题目内容
7.已知点M(1,0)及双曲线$\frac{{x}^{2}}{3}$-y2=1的右支上两动点A,B,当∠AMB最大时,它的余弦值为$\frac{1}{3}$.分析 根据题意,当直线MA、MB分别与双曲线相切于点A、B时,可得∠AMB取得最大值.建立方程组关系进行求解即可.
解答 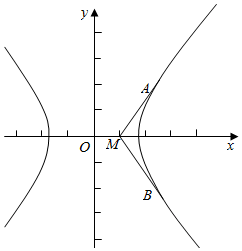 解:当直线MA与双曲线相切于点A,直线MB与双曲线相切于点B时,
解:当直线MA与双曲线相切于点A,直线MB与双曲线相切于点B时,
∠AMB取得最大值.
设直线AM方程为y=k(x-1),与双曲线消去y,
($\frac{1}{3}$-k2)x2+2k2x-k2-1=0
∵直线MA与双曲线相切于点A,
∴(2k2)2-4×($\frac{1}{3}$-k2)×(-k2-1)=0,解之得k=$\frac{\sqrt{2}}{2}$(舍负)
因此,直线AM方程为y=$\frac{\sqrt{2}}{2}$(x-1),
同理直线BM方程为y=-$\frac{\sqrt{2}}{2}$(x-1),
设直线AM倾斜角为θ,得tanθ=$\frac{\sqrt{2}}{2}$,且∠AMB=2θ
∴cos2θ=$\frac{1-ta{n}^{2}θ}{1+ta{n}^{2}θ}$=$\frac{1-\frac{1}{2}}{1+\frac{1}{2}}$=$\frac{1}{3}$,
即为∠AMB最大时的余弦值
故答案为:$\frac{1}{3}$
点评 本题给出双曲线方程和性质,着重考查了双曲线的简单几何性质和直线与双曲线的位置关系等知识,属于中档题.

练习册系列答案
相关题目
17.已知a=log23,b=log32,c=log0.52,那么( )
| A. | a<b<c | B. | a<c<b | C. | c<b<a | D. | b<c<a |
16.如果角β的终边过点P(-5,12),则sinβ+cosβ+tanβ的值为( )
| A. | $\frac{47}{13}$ | B. | -$\frac{121}{65}$ | C. | -$\frac{47}{13}$ | D. | $\frac{121}{65}$ |
17.若直线x=$\frac{π}{3}$是函数f(x)=sin(2x+φ)(其中|φ|<$\frac{π}{2}$)的图象的一条对称轴,则φ的值为( )
| A. | -$\frac{π}{3}$ | B. | -$\frac{π}{6}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{3}$ |