题目内容
已知圆 .
.
(1)若圆 的切线在
的切线在 轴和
轴和 轴上的截距相等,且截距不为零,求此切线的方程;
轴上的截距相等,且截距不为零,求此切线的方程;
(2)从圆 外一点
外一点 向该圆引一条切线,切点为
向该圆引一条切线,切点为 ,
, 为坐标原点,且有
为坐标原点,且有 ,求使
,求使
的长取得最小值的点 的坐标.
的坐标.
解析:(1) 切线在两坐标轴上的截距相等且截距不为零,
切线在两坐标轴上的截距相等且截距不为零,
 设切线方程为
设切线方程为 ,(
,( )
)
又 圆C:
圆C: ,
, 圆心C
圆心C 到切线的距离等于圆的半径
到切线的距离等于圆的半径 ,
,


则所求切线的方程为: . ………………4分
. ………………4分
(2)设 ,
, 切线
切线 与半径
与半径 垂直,
垂直,



 动点
动点 在直线
在直线 上, ………………6分
上, ………………6分
由已知 的最小值就是
的最小值就是 的最小值,
的最小值,
而 的最小值为
的最小值为 到直线
到直线 的距离
的距离 ,………8分
,………8分


 所求点坐标为
所求点坐标为 .
.

练习册系列答案
相关题目
 中,
中, 分别是与x轴,y轴平行的单位向量,若直角三角形ABC中,
分别是与x轴,y轴平行的单位向量,若直角三角形ABC中, ,则实数m=________________.
,则实数m=________________. 的一个焦点,则m= .
的一个焦点,则m= .  在区间
在区间 内有一个零点,则实数
内有一个零点,则实数 的取值可以是
的取值可以是 B.
B. C..
C.. D.
D.
 ,
, .
. ,求
,求 ;
; ,求实数
,求实数 ,它们的夹角是60°,
,它们的夹角是60°, 与
与 、
、 向量的夹角都为
向量的夹角都为 ,且|
,且| ,若
,若 ,则
,则 值为( )
值为( )

 的值域为
的值域为 ,则
,则 的最小值为 .
的最小值为 . 且函数
且函数 的零点均在区间
的零点均在区间
 内,圆
内,圆 的面积的最小值是( )
的面积的最小值是( )

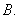

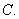

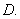

 为抛物线
为抛物线 上的动弦,且
上的动弦,且 , 则弦
, 则弦 到
到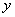 轴的最小距离
轴的最小距离 C. 1 D.
C. 1 D. 