题目内容
(本题满分14分)已知函数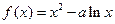 (常数
(常数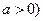 .
.
(Ⅰ) 当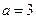 时,求曲线
时,求曲线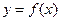 在点
在点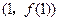 处的切线方程;
处的切线方程;
(Ⅱ)讨论函数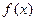 在区间
在区间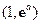 上零点的个数(
上零点的个数(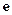 为自然对数的底数).
为自然对数的底数).
解:(Ⅰ)当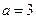 时,
时,
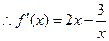 . …1分
. …1分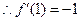 . 又
. 又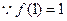 ,
,
∴曲线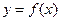 在点
在点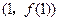 处的切线方程为
处的切线方程为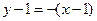 .即
.即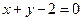 .…3分
.…3分
(Ⅱ)(1)下面先证明: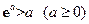 .
.
设 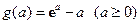 ,则
,则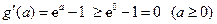 ,
,
且仅当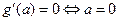 ,所以,
,所以,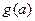 在
在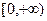 上是增函数,故
上是增函数,故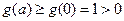 .
.
所以, ,即
,即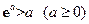 . …………………………5分
. …………………………5分
(2)因为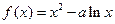 ,所以
,所以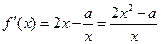
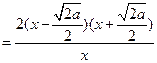 .
.
因为当 时,
时,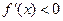 ,当
,当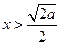 时,
时, .
.
又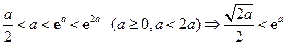 ,所以
,所以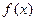 在
在 上是减函数,在
上是减函数,在 上是增函数.所以,
上是增函数.所以, …9分
…9分
(3)下面讨论函数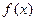 的零点情况.
的零点情况.
①当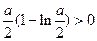 ,即
,即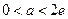 时,函数
时,函数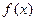 在
在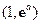 上无零点;
上无零点;
②)当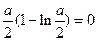 ,即
,即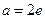 时,
时,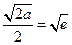 ,则
,则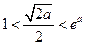
而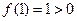 ,
,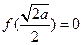
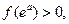 ∴
∴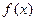 在
在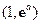 上有一个零点;
上有一个零点;
③当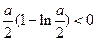 ,即
,即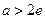 时,
时,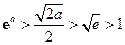 ,
,
由于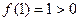 ,
, ,
,
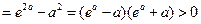 ,
,
所以,函数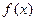 在
在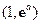 上有两个零点. ……………………………………13分
上有两个零点. ……………………………………13分
综上所述,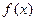 在
在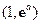 上,我们有结论:当
上,我们有结论:当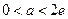 时,函数
时,函数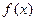 无零点;当
无零点;当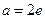 时,函数
时,函数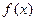 有一个零点;当
有一个零点;当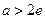 时,函数
时,函数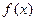 有两个零点. ………………………………14分
有两个零点. ………………………………14分
解法二:(Ⅱ)依题意,可知函数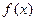 的定义域为
的定义域为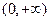 ,
,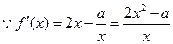
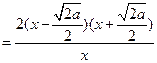 . ………5分
. ………5分
∴当 时,
时,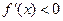 ,当
,当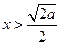 时,<
时,<
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 是奇函数,且图像在点
是奇函数,且图像在点
 为自然对数的底数)处的切线斜率为3.
为自然对数的底数)处的切线斜率为3. 、
、 的值;
的值; ,且
,且 对任意
对任意 恒成立,求
恒成立,求 的最大值;
的最大值; 时,证明:
时,证明:

 的单调减区间;
的单调减区间; 满足,
满足, 求证:
求证: ;
; ,
, 为数列
为数列 的前
的前 项和,求证:
项和,求证: 。
。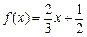 ,
,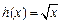 .
.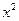 [h(x)]
[h(x)]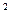 ,求F(x)的单调区间与极值;
,求F(x)的单调区间与极值;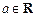 ,解关于x的方程
,解关于x的方程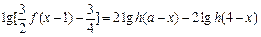 ;
;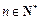 ,证明:
,证明: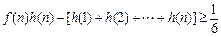 .
. 在
在 上是增函数,在
上是增函数,在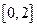 上是减函数,且方程
上是减函数,且方程 有三个根,它们分别是
有三个根,它们分别是 .
.  的值; (2)求证:
的值; (2)求证:  (3)求
(3)求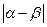 的取值范围.
的取值范围. (吨)与每吨产品的价格p(元/吨)之间的关系式为:p=24200-0.2x2,且生产x吨的成本为
(吨)与每吨产品的价格p(元/吨)之间的关系式为:p=24200-0.2x2,且生产x吨的成本为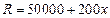 (元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(注:利润=收入─成本)
(元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(注:利润=收入─成本)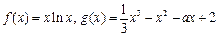 .
.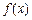 的单调区间;
的单调区间;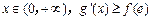 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围. 分13分)已知
分13分)已知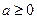 ,函数
,函数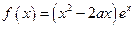 .
.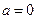 时讨论函数的单调性;
时讨论函数的单调性;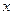 取何值时,
取何值时,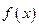 取最小值,证明你的结论.
取最小值,证明你的结论.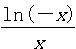 ,其中e是自然常数,a∈R.
,其中e是自然常数,a∈R. x)的单调性、极值;
x)的单调性、极值;