题目内容
在平面直角坐标系中,以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线 的极坐标方程为
的极坐标方程为 ,过点
,过点 的直线
的直线 的参数方程为
的参数方程为 (
( 为参数),直线
为参数),直线 与曲线
与曲线 相交于
相交于 两点.
两点.
(Ⅰ)写出曲线 的直角坐标方程和直线
的直角坐标方程和直线 的普通方程;
的普通方程;
(Ⅱ)若 ,求
,求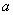 的值
的值
解:(1) 由ρsin2θ=2acosθ(a>0)得ρ2sin2θ=2aρcosθ(a>0)
∴曲线C的直角坐标方程为y2=2ax(a>0)………………………2分
直线l的普通方程为y=x-2…………………………………4分
(2)将直线l的参数方程代入曲线C的直角坐标方程y2=2ax中,
得t2-2 (4+a)t+8(4+a)=0
(4+a)t+8(4+a)=0
设A、B两点对应的参数分别为t1、t2
则有t1+t2=2 (4+a), t1t2=8(4+a)……………………………6分
(4+a), t1t2=8(4+a)……………………………6分
∵|PA|×|PB|=|AB|2,∴t1t2=(t1-t2)2, 即(t1+t2)2=5t1t2……………8分
∴[2 (4+a)]2=40(4+a),即a2+3a-4=0
(4+a)]2=40(4+a),即a2+3a-4=0
解之得:a=1或a=-4(舍去),∴a的值为1…………………10分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的各项均为正数,且
的各项均为正数,且 成等差数列,
成等差数列, 成等比数列.
成等比数列. ,记
,记 ,
, ,求证:
,求证:
 满足:
满足: ,且对于任意的
,且对于任意的 ,都有
,都有 ,则不等式
,则不等式 的解集为 __________________
的解集为 __________________ 的值为6,那么运行相应程序,输出的
的值为6,那么运行相应程序,输出的 的值为( )
的值为( )
 中,角
中,角 所对边分别为
所对边分别为 ,已知
,已知 .
. 的值;
的值; 求
求 的值.
的值. 对称的点的坐标是
对称的点的坐标是 ,则
,则 = .
= . 过定点
过定点 ,且与以
,且与以 ,
, 为端点的线段(包含端点)有交点,则直线
为端点的线段(包含端点)有交点,则直线 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.