题目内容

（2012•泰安一模）若|
b
丨=2|
a
|≠0，
c
=
a
+
b
，且
c
⊥
a
，则向量
a
与
b
的夹角为（　　）
分析：利用向量垂直的充要条件及向量的数量积公式列出方程，求出夹角余弦，从而求出夹角．
解答：解：设
a
，
b
的夹角为θ
∵
c
⊥
a
，∴
c
•
a
=0
∴（
a
+
b
）•
a
=0即
a
2+
a
•
b
=0
∴|
a
|2+|
a
||
b
||cosθ=0
∵|
b
=2|
a
|≠0
∴1+2cosθ=0
∴cosθ=-
1
2

∴θ=120°
故选：C．
点评：本题考查两个向量的数量积的定义以及两个向量垂直的条件．考察基础知识，属于基础题目．
练习册系列答案
相关题目
（2012•泰安一模）在△ABC中，角A、B、C所对应的边分别为a、b、c，且满足2acosB=bcosC+ccosB．
（I）求角B的大小；
（II）求函数f(A)=2sin2(A+
π
4
)-cos(2A+
π
6
)的最大值及取得最大值时的A值．
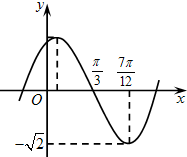（2012•泰安一模）函数f（x）=Asin（ωx+?）（A，ω，?为常数，A＞0，ω＞0）的部分图象如图所示，则f(
π
6
)的值是
6
2
6
2
．
（2012•泰安一模）若a、b为实数，则“ab＜1”是“0＜a＜
1
b
”的（　　）
（2012•泰安一模）已知Ω={（x，y）||x≤1，|y|≤1}，A是曲线y=x2与y=x
1
2
围成的区域，若向区域Ω上随机投一点P，则点P落入区域A的概率为（　　）
（2012•泰安一模）设P={y|y=-x2+1，x∈R}，Q={y|y=2x，x∈R}，则（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网