题目内容

11．边长为1的正方体ABCD-A1B1C1D1若将其对角线AC1与平面α垂直，则正方体ABCD-A1B1C1D1在平面α上的投影面积为$\sqrt{3}$．

分析 根据题意，画出图形，找出与AC1垂直的平面去截正方体ABCD-A1B1C1D1所得的截面是什么，
再求正方体在该平面上的投影面积．

解答 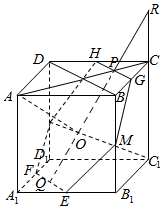解：如图所示，
连接BB1，DD1的中点MN，交AC1于点O，
在对角面ACC1A1中，过点O作OP⊥AC，交AC1于点P，
则平面MOP是对角线AC1的垂面；
该平面截正方体ABCD-A1B1C1D1所得的截面是六边形MGHNFE；
则正方体在该平面上的投影面积是$\frac{1}{2}$MN•2OR=$\frac{1}{2}$×$\sqrt{2}$×2×$\frac{\sqrt{6}}{2}$=$\sqrt{3}$．
故答案为：$\sqrt{3}$．

点评 本题考查了空间几何体的应用问题，也考查了空间想象能力与逻辑推理能力的应用问题．

练习册系列答案
相关题目
1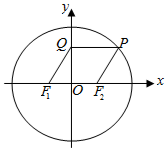．如图，椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的左、右焦点分别为F1，F2，过椭圆上的点P作y轴的垂线，垂足为Q，若四边形F1F2PQ为菱形，则该椭圆的离心率为（　　）
A．$\frac{{\sqrt{2}-1}}{2}$B．$\frac{{\sqrt{3}-1}}{2}$C．$\sqrt{2}-1$D．$\sqrt{3}-1$
2．已知函数f（x）=x3-$\frac{1}{2}$x2+bx+c，若f（x）在R上是增加的，求实数b的最小值．
19．设函数f（x）=exlnx+$\frac{2{e}^{x-1}}{x}$，证明f（x）＞1．
6．给出下列命题：
①双曲线$\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{9}$=1与椭圆$\frac{{x}^{2}}{35}$+y2=1有相同的焦点；
②过点P（2，1）的抛物线的标准方程是y2=$\frac{1}{2}$x；
③已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1，若它的离心率为$\sqrt{5}$，则双曲线C的一条渐近线方程为y=2x；
④椭圆$\frac{{x}^{2}}{m+1}$+$\frac{{y}^{2}}{m}$=1的两个焦点为F1，F2，P为椭圆上的动点，△PF1F2的面积的最大值为2，则m的值为2．
其中真命题的序号为①③．（写出所有真命题的序号）
16．若a=$\frac{1-cosα}{sinα}$，b=$\frac{1+cosα}{sinα}$，则ab的值是（　　）
A．0B．1C．-1D．$\sqrt{2}$
3．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0）的离心率为$\frac{\sqrt{3}}{2}$，且点（$\sqrt{2}$，$\frac{\sqrt{2}}{2}$）在C上．
（1）求椭圆C的方程；
（2）直线l经过点P（1，0），且与椭圆C有两个交点A，B，是否存在直线l0：x=x0（其中x0＞2），问A，B到l0的距离dA，dB满足：$\frac{{d}_{A}}{{d}_{B}}$=$\frac{|PA|}{|PB|}$恒成立？若存在，求x0的值；若不存在，请说明理由．
20．已知函数f（x）=x-alnx+$\frac{1-a}{x}$（a∈R），g（x）=x-1．
（Ⅰ）若函数f（x）在x=2处取得极值，求实数a的值；
（Ⅱ）是否存在a∈（3，+∞），对任意x1$∈[\frac{1}{e}，1]$，总存在x2$∈[\frac{1}{e}，1]$，使得g（x1）=f（x2）成立．若存在，求出a的范围；若不存在，请说明理由．
1．已知公差大于零的等差数列{an}的前n项和为Sn，且满足a3a4=117，a2+a5=22．
（1）求{an}的通项公式．
（2）等差数列{bn}的通项公式为bn=$\frac{{S}_{n}}{n+c}$，求非零常数c的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网