题目内容
已知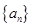 为公差不为零的等差数列,首项
为公差不为零的等差数列,首项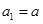 ,
,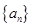 的部分项
的部分项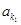 、
、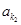 、
、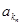 恰为等比数列,且
恰为等比数列,且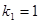 ,
,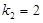 ,
,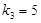 .
.
(1)求数列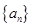 的通项公式
的通项公式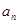 (用
(用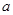 表示);
表示);
(2)若数列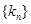 的前
的前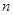 项和为
项和为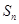 ,求
,求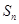 .
.
(1)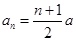 (2)Sn
(2)Sn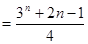
解析试题分析:
(1)由题得a1,a5,a17是成等比数列的,所以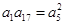 ,则根据
,则根据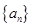 为等差数列,所以可以利用公差d和首项a来表示
为等差数列,所以可以利用公差d和首项a来表示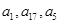 ,进而利用
,进而利用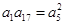 求的到d的值(利用a来表示),得到an的通项公式.
求的到d的值(利用a来表示),得到an的通项公式.
(2)利用第一问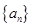 的通项公式可以求的等比数列
的通项公式可以求的等比数列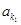 、
、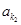 、 、
、 、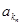 中的前三项,得到该等比数列
中的前三项,得到该等比数列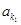 、
、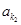 、 、
、 、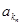 的公比与首项,进而得到
的公比与首项,进而得到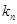 的通项公式
的通项公式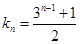 ,则
,则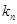 为等比数列与常数数列的和,故利用分组求和法可得到Sn的表达式.
为等比数列与常数数列的和,故利用分组求和法可得到Sn的表达式.
试题解析:
(1)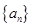 为公差不为
为公差不为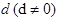 ,由已知得
,由已知得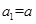 ,
,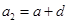 ,
,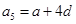 成等比数列,
成等比数列,
∴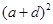
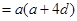 , 1分
, 1分
得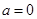 或
或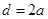 2分
2分
若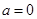 ,则
,则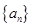 为
为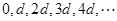 ,这与
,这与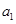 ,
,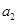 ,
,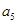 成等比数列矛盾,
成等比数列矛盾,
所以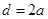 , 4分
, 4分
所以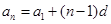
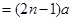 . 5分
. 5分
(2)由(1)可知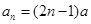
∴ 7分
7分
而等比数列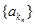 的公比
的公比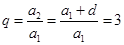 。
。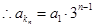 9分
9分
因此
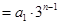 ,
,
∴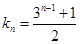
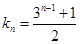
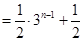 11分
11分
∴ 
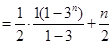
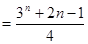 14分
14分
考点: 等比数列 等比数学 分组求和

练习册系列答案
相关题目
 }的公差
}的公差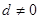 ,
,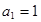 ,且
,且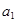 ,
,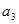 ,
,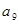 成等比数列.
成等比数列.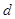 及通项
及通项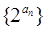 的前
的前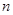 项和
项和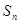 .
.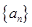 中,
中,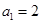 ,
,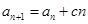 (
(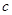 是常数,
是常数,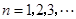 ),且
),且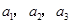 成公比不为
成公比不为 的等比数列.
的等比数列.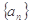 中,
中,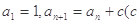 为常数,
为常数,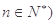 ,且
,且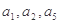 成公比不等于1的等比数列
成公比不等于1的等比数列 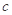 的值;
的值;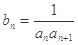 ,求数列
,求数列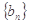 的前
的前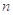 项和
项和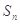
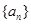 ,其前
,其前 项和
项和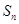 满足
满足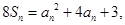 且
且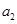 是
是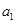 和
和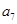 的等比中项..
的等比中项..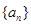 的通项公式;
的通项公式;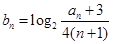 ,求数列
,求数列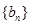 的前99项和.
的前99项和. (n∈N*),若Tn+
(n∈N*),若Tn+ <c(c∈Z)恒成立,求c的最小值.
<c(c∈Z)恒成立,求c的最小值.