题目内容
已知正项数列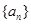 ,其前
,其前 项和
项和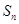 满足
满足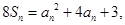 且
且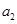 是
是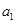 和
和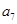 的等比中项..
的等比中项..
(1)求数列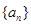 的通项公式;
的通项公式;
(2)设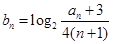 ,求数列
,求数列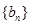 的前99项和.
的前99项和.
(1) 所以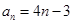 ;(2)
;(2) 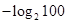 .
.
解析试题分析:(1) 由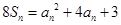 ①
①
知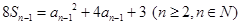 ②
②
通过① ②得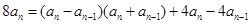
整理得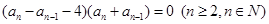 ,
,
根据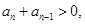 得到
得到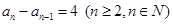
所以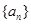 为公差为
为公差为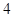 的等差数列,由
的等差数列,由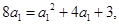 求得
求得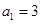 或
或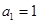 .验证舍去
.验证舍去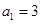 .
.
(2) (2) 由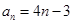 得
得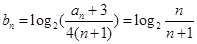 ,利用对数的运算法则,将
,利用对数的运算法则,将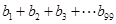 转化成
转化成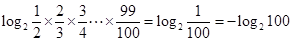 .
.
试题解析:(1) 由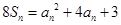 ①
①
知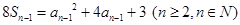 ② 1分
② 1分
由① ②得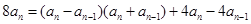
整理得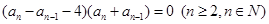 2分
2分
∵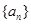 为正项数列∴
为正项数列∴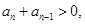 ,∴
,∴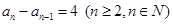 3分
3分
所以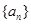 为公差为
为公差为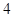 的等差数列,由
的等差数列,由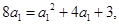 得
得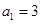 或
或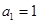 4分
4分
当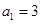 时,
时,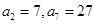 ,不满足
,不满足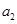 是
是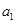 和
和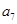 的等比中项.
的等比中项.
当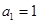 时,
时,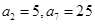 ,满足
,满足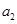 是
是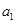 和
和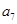 的等比中项.
的等比中项.
所以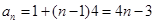 . 6分
. 6分
(2) 由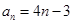 得
得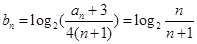 , 8分
, 8分
所以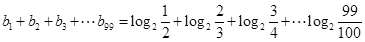 10分
10分 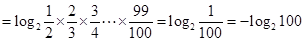 12分
12分
考点:等差数列的通项公式,对数运算,数列的求和.

练习册系列答案
相关题目
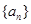 中,已知
中,已知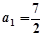 ,
,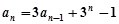 (
(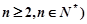 .
.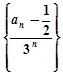 是等差数列;
是等差数列;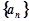 的通项公式
的通项公式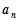 及它的前
及它的前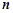 项和
项和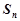 .
.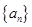 的前
的前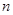 项和为
项和为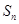 ,且
,且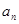 和
和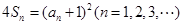 .
.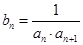 ,求
,求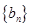 的前
的前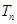 ;
;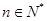 ,
,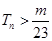 都成立,求整数
都成立,求整数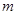 的最大值.
的最大值.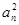 }成等差数列.
}成等差数列.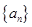 是公比为
是公比为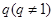 的等比数列,且
的等比数列,且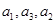 成等差数列.
成等差数列.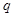 的值;
的值;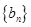 是以
是以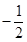 为首项,
为首项,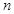 项和
项和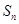 .
.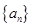 为公差不为零的等差数列,首项
为公差不为零的等差数列,首项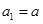 ,
,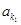 、
、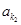 、
、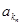 恰为等比数列,且
恰为等比数列,且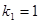 ,
,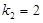 ,
,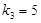 .
.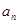 (用
(用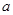 表示);
表示);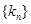 的前
的前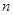 项和为
项和为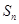 ,求
,求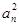 -(2n-1)an-2n=0.
-(2n-1)an-2n=0.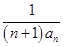 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.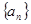 的公差大于0,且
的公差大于0,且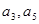 是方程
是方程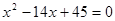 的两根,数列
的两根,数列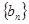 的前n项的和为
的前n项的和为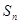 ,且
,且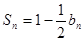 .
.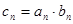 ,求证:
,求证: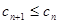 .
.