题目内容
8.以抛物线y2=8x的焦点为圆心,以双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的虚半轴长b为半径的圆与该双曲线的渐近线相切,则当$\frac{4}{a^2}+\frac{1}{b^2}$取得最小值时,双曲线的离心率为$\frac{\sqrt{6}}{2}$.分析 利用以抛物线y2=8x的焦点为圆心,以双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的虚半轴长b为半径的圆与该双曲线的渐近线相切,求出a2+b2=4,再利用基本不等式,得出当且仅当a=2b时,$\frac{4}{a^2}+\frac{1}{b^2}$取得最小值,即可求出双曲线的离心率.
解答 解:抛物线y2=8x的焦点为(2,0),双曲线的一条渐近线方程为bx+ay=0,
∵以抛物线y2=8x的焦点为圆心,以双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$
的虚半轴长b为半径的圆与该双曲线的渐近线相切,
∴$\frac{2b}{\sqrt{{b}^{2}+{a}^{2}}}$=b,∴a2+b2=4,
∴$\frac{4}{a^2}+\frac{1}{b^2}$=$\frac{1}{4}$($\frac{4}{a^2}+\frac{1}{b^2}$)(a2+b2)=$\frac{1}{4}$(5+$\frac{4{b}^{2}}{{a}^{2}}$+$\frac{{a}^{2}}{{b}^{2}}$)≥$\frac{1}{4}$(5+4)=$\frac{9}{4}$,
当且仅当a=$\sqrt{2}$b时,$\frac{4}{a^2}+\frac{1}{b^2}$取得最小值,∴c=$\sqrt{3}$b,
∴e=$\frac{c}{a}$=$\frac{\sqrt{3}b}{\sqrt{2}b}$=$\frac{\sqrt{6}}{2}$.
故答案为$\frac{\sqrt{6}}{2}$.
点评 本题考查抛物线的性质,考查直线与圆的位置关系,考查基本不等式的运用,属于中档题.

| A. | $({-\frac{3}{2},-\frac{3}{2e}})$ | B. | $[{-\frac{3}{2e},-\frac{5}{{3{e^2}}}})$ | C. | $[{-\frac{3}{2},-\frac{5}{{3{e^2}}}})$ | D. | $[{-2e,-\frac{3}{2e}})$ |
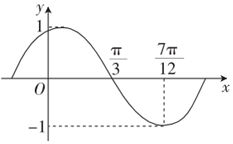 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$),其部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$),其部分图象如图所示.