题目内容
已知集合A={x∈R||x+1|+|x-2|≤5},非空集合B={x∈R|2a≤x≤a+3},若B⊆A,则实数a的取值范围是 .
考点:集合的包含关系判断及应用
专题:计算题,集合
分析:解绝对值不等式求出A,进而根据非空集合B={x∈R|2a≤x≤a+3}满足B⊆A,构造关于a的不等式组,解不等式组可得答案.
解答:
解:∵集合A={x∈R||x+1|+|x-2|≤5}=[-2,3],
由集合B不为空集可得2a≤a+3,即a≤3时,
由B⊆A得
,
解得a∈[-1,0],
故答案为:[-1,0].
由集合B不为空集可得2a≤a+3,即a≤3时,
由B⊆A得
|
解得a∈[-1,0],
故答案为:[-1,0].
点评:本题考查的知识点是集合的包含关系判断及应用,其中根据集合包含的定义,构造关于a的不等式组,是解答的关键.

练习册系列答案
相关题目
一数字游戏规则如下:第1次生成一个数a,以后每次生成的结果均是由上一次生成的每一个数x生成两个数,一个是-x,另一个是x+2.设前n次生成的所有数的和为Sn,若a=1,则S6=( )
| A、32 | B、64 |
| C、127 | D、128 |
已知X={x|x=2n+1,n∈Z},Y={y|y=4k±1,k∈Z},那么下列各式正确的是( )
| A、X?Y | B、Y?X |
| C、X=Y | D、以上都不对 |
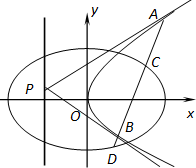 已知中心在原点的椭圆Γ1和抛物线Γ2有相同的焦点(1,0),椭圆Γ1的离心率为
已知中心在原点的椭圆Γ1和抛物线Γ2有相同的焦点(1,0),椭圆Γ1的离心率为