题目内容
16．若x．y满足约束条件$\left\{\begin{array}{l}{x+2y-2≥0}\\{x-y+1≥0}\\{2x-y-2≤0}\end{array}\right.$，则u=log2（3x+y）的取值范围是[0，${log}_{2}^{13}$．分析 画出满足条件的平面区域，求出角点的坐标，令z=3x+y，则y=-3x+z，从而求出u的范围即可．
解答 解：画出满足条件的平面区域，如图示：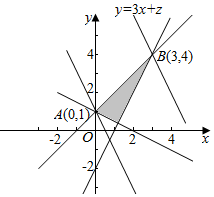
，
由$\left\{\begin{array}{l}{x-y+1=0}\\{2x-y-2=0}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$，
∴B（3，4），
令z=3x+y，则y=-3x+z，
显然直线过A时，z最小，最小值是1，
过B时z最大，最大值是13，
故0≤log2（3x+y）≤${log}_{2}^{13}$，
故答案为：[0，${log}_{2}^{13}$．
点评 本题考查了简单的线性规划问题，考查数形结合思想，是一道中档题．
练习册系列答案
相关题目
6．△ABC的三内角A，B，C所对边分别为a，b，c，若a2+b2-c2=ab，则角C的大小为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{2}$ | D． | $\frac{2π}{3}$ |
5．已知α∈[$\frac{π}{6}$，$\frac{2}{3}$π]，点A在角α的终边上，且|OA|=4sinα，则点A纵坐标的取值范围是（ ）
| A． | [2，2$\sqrt{3}$] | B． | [2，3] | C． | [2，4] | D． | [1，4] |
如图，四棱锥P-ABCD的底面为正方形，PA⊥底面ABCD，PA=AD．E，F分别为底边AB和侧棱PC的中点．