题目内容
已知tan(
+α)=
,则
的值为( )
| π |
| 4 |
| 1 |
| 2 |
| sin2α-cos2α |
| 1+cos2α |
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
考点:同角三角函数基本关系的运用
专题:计算题,三角函数的求值
分析:利用两角和的正切可求得tanα=-
,再利用倍角公式将所求关系式化简整理后,将tanα=-
代入计算即可.
| 1 |
| 3 |
| 1 |
| 3 |
解答:
解:∵tan(
+α)=
=
=
,
∴3tanα=-1,
解得:tanα=-
;
∴
=
=tanα-
=-
-
=-
.
故选:B.
| π |
| 4 |
tan
| ||
1-tan
|
| 1+tanα |
| 1-tanα |
| 1 |
| 2 |
∴3tanα=-1,
解得:tanα=-
| 1 |
| 3 |
∴
| sin2α-cos2α |
| 1+cos2α |
| 2sinαcosα-cos2α |
| 2cos2α |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 6 |
故选:B.
点评:本题考查同角三角函数基本关系的运用,求得利用两角和的正切求得tanα=-
是关键,考查化简求解能力,属于中档题.
| 1 |
| 3 |

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
一个几何体的三视图如图所示,则该几何体的体积为( )


| A、2 | ||
| B、1 | ||
C、
| ||
D、
|
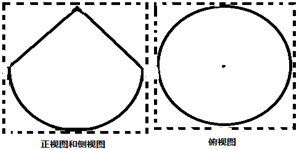 如图实线所示,一个几何体的正视图和侧视图相同,俯视图为圆形,该几何体的三视图恰好可放在边长为2的正方形内(图中虚线所示),则该几何体的体积为( )
如图实线所示,一个几何体的正视图和侧视图相同,俯视图为圆形,该几何体的三视图恰好可放在边长为2的正方形内(图中虚线所示),则该几何体的体积为( )A、1+
| ||
| B、2+π | ||
| C、π | ||
D、
|
若双曲线
-
=1的离心率为2,则实数m的值为( )
| x2 |
| 2 |
| y2 |
| m |
A、2
| ||
| B、3 | ||
C、
| ||
| D、6 |
已知P(
,
)在角α的终边上,则sinα的值是( )
| 1 |
| 2 |
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
抛物线y2=20x的焦点坐标为( )
| A、(10,0) |
| B、(5,0) |
| C、(0,10) |
| D、(0,5) |
下列函数中,既不是奇函数又不是偶函数,且在(-∞,0)上是增函数的是( )
| A、f(x)=5x+2 | ||
B、f(x)=
| ||
C、f(x)=
| ||
| D、f(x)=x2 |