题目内容
【题目】如图,在![]() 中,
中, ![]() ,角
,角![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() ,设
,设![]() .(1)求
.(1)求![]() ;(2)若
;(2)若![]() ,求
,求![]() 的长.
的长.

【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)由α为三角形BAD中的角,根据sinα的值,利用同角三角函数间的基本关系求出cosα的值,进而利用二倍角的正弦函数公式求出sin∠BAC与cos∠BAC的值,即为sin2α与cos2α的值,sinC变形为![]() ,利用诱导公式,以及两角和与差的正弦函数公式化简后,将各自的值代入计算即可求出sinC的值;
,利用诱导公式,以及两角和与差的正弦函数公式化简后,将各自的值代入计算即可求出sinC的值;
(2)利用正弦定理列出关系式,将sinC与sin∠BAC的值代入得出![]() ,利用平面向量的数量积运算法则化简已知等式左边,将表示出的AB代入求出BC的长,再利用正弦定理即可求出AC的长.
,利用平面向量的数量积运算法则化简已知等式左边,将表示出的AB代入求出BC的长,再利用正弦定理即可求出AC的长.
试题解析:
解:(1)∵![]() ,
, ![]() ,
,
∴![]() ,
,
则![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)由正弦定理,得![]() ,即
,即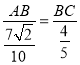 ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() ,由上两式解得
,由上两式解得![]() ,
,
又由![]() 得
得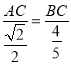 ,∴
,∴![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目