题目内容
【题目】(本小题满分12分)已知抛物线![]() 的顶点在坐标原点
的顶点在坐标原点![]() ,对称轴为
,对称轴为![]() 轴,焦点为
轴,焦点为![]() ,抛物线上一点
,抛物线上一点![]() 的横坐标为
的横坐标为![]() ,且
,且![]() .
.
(Ⅰ)求此抛物线![]() 的方程;
的方程;
(Ⅱ)过点![]() 做直线
做直线![]() 交抛物线
交抛物线![]() 于
于![]() 两点,求证:
两点,求证:![]() .
.
【答案】(Ⅰ)![]()
(Ⅱ)证明过程见解析.
【解析】
试题分析:对于第一问,根据题意,设出相应的点的坐标,应用点在曲先上,满足曲线的方程,向量垂直应用向量的数量积等于零,构造出相应的方程,从而求出p的值,进而得到抛物线的方程;对于第二问,把握住垂直关系由向量的数量积等于零来体现,注意对直线的斜率不存在的时候的验证,主要就是关于直线和曲线相交,联立方程组过程要熟练.
试题解析:(Ⅰ)设![]() ,点
,点![]() ,则有
,则有![]() 1分
1分
![]() 3分
3分
![]() ,所以抛物线
,所以抛物线![]() 的方程为
的方程为![]() . 5分
. 5分
(Ⅱ)当直线![]() 斜率不存在时,此时
斜率不存在时,此时![]() ,解得
,解得![]()
满足![]() 7分
7分
当直线![]() 斜率存在时,设
斜率存在时,设![]() ,
,
联立方程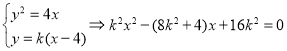
设![]() ,则
,则![]() 9分
9分
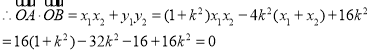
![]() 11分
11分
综上,![]() 成立. 12分
成立. 12分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目