题目内容
【题目】已知函数![]() .
.
(I)讨论函数![]() 在
在![]() 上的单调性;
上的单调性;
(II)设函数![]() 存在两个极值点,并记作
存在两个极值点,并记作![]() ,若
,若![]() ,求正数
,求正数![]() 的取值范围;
的取值范围;
(III)求证:当![]() =1时,
=1时, ![]() (其中e为自然对数的底数)
(其中e为自然对数的底数)
【答案】(1)当![]() 时,函数
时,函数![]() 在
在![]() 上是增函数;当
上是增函数;当![]() 时,函数
时,函数![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数.(2)正数
上是增函数.(2)正数![]() 的取值范围是
的取值范围是![]() .(3)见解析
.(3)见解析
【解析】试题分析:(1)先求函数导数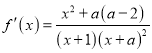 ,,再讨论导函数在定义区间上符号变化规律:当
,,再讨论导函数在定义区间上符号变化规律:当![]() 时,
时, ![]() ,即在
,即在![]() 上是增函数;当
上是增函数;当![]() 时,导函数有一个零点,符号先负后正,对应区间先减后增,(2)由题意易得要使函数
时,导函数有一个零点,符号先负后正,对应区间先减后增,(2)由题意易得要使函数![]() 存在两个极值点,必有
存在两个极值点,必有![]() ,且极值点必为
,且极值点必为![]() ,
, ![]() ,因此
,因此![]() ,即正数
,即正数![]() 的取值范围是
的取值范围是![]() .再化简条件
.再化简条件![]() ,得
,得![]() ,利用导数研究其单调性:为单调减,因此正数
,利用导数研究其单调性:为单调减,因此正数![]() 的取值范围是
的取值范围是![]() .(3)要证不等式
.(3)要证不等式![]() ,即证
,即证![]() ,利用导数易得函数
,利用导数易得函数![]() 最小值为1,而
最小值为1,而![]() ,得证.
,得证.
试题解析:(Ⅰ)  ,(
,( ![]() )
)
当![]() 时,
时, ![]() ,
, ![]()
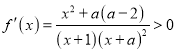 ,函数
,函数![]() 在
在![]() 上是增函数;
上是增函数;
当![]() 时,由
时,由![]() ,得
,得![]() ,解得
,解得![]() (负值舍去),
(负值舍去),![]() ,所以
,所以
当![]() 时,
时, ![]() ,从而
,从而![]() ,函数
,函数![]() 在
在![]() 上是减函数;
上是减函数;
当![]() 时,
时, ![]() ,从而
,从而![]() ,函数
,函数![]() 在
在![]() 上是增函数.
上是增函数.
综上,当![]() 时,函数
时,函数![]() 在
在![]() 上是增函数;
上是增函数;
当![]() 时,函数
时,函数![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数.
上是增函数.
(Ⅱ)由(Ⅰ)知,当![]() 时,
时, ![]() ,函数
,函数![]() 无极值点;
无极值点;
要使函数![]() 存在两个极值点,必有
存在两个极值点,必有![]() ,且极值点必为
,且极值点必为![]() ,
, ![]() ,又由函数定义域知,
,又由函数定义域知, ![]() ,则有
,则有![]() ,即
,即
![]() ,化为
,化为![]() ,所以
,所以![]() ,
,
所以,函数![]() 存在两个极值点时,正数
存在两个极值点时,正数![]() 的取值范围是
的取值范围是![]() .
.
由(![]() )式可知,
)式可知, ![]()
![]()
![]()
![]()
![]()
不等式![]() 化为
化为![]() ,
,
令![]() ,所以
,所以![]() ,
,
令![]() ,
, ![]() .
.
当![]() 时,
时, ![]() ,
, ![]() ,所以
,所以![]() ,不合题意;
,不合题意;
当![]() 时,
时, ![]() ,
, ![]() ,所以
,所以
![]() 在
在![]() 是减函数,所以
是减函数,所以![]() ,适合题意,即
,适合题意,即![]() .
.
综上,若![]() ,此时正数
,此时正数![]() 的取值范围是
的取值范围是![]() .
.
(Ⅲ)当![]() 时,
时, ![]() ,
,
不等式![]() 可化为
可化为![]() ,所以
,所以
要证不等式![]() ,即证
,即证![]() ,即证
,即证![]() ,
,
设![]() ,则
,则![]() ,
,
在![]() 上,h'(x)<0,h(x)是减函数;
上,h'(x)<0,h(x)是减函数;
在![]() 上,h'(x)>0,h(x)是增函数.
上,h'(x)>0,h(x)是增函数.
所以![]() ,
,
设![]() ,则
,则![]() 是减函数,
是减函数,
所以![]() ,
,
所以![]() ,即
,即![]() ,
,
所以当![]() 时,不等式
时,不等式![]() 成立.
成立.

【题目】定义在R上的奇函数f(x),当x∈(﹣∞,0)时,f(x)=﹣x2+mx﹣1.
(1)当x∈(0,+∞)时,求f(x)的解析式;
(2)若方程f(x)=0有五个不相等的实数解,求实数m的取值范围.
【题目】孝感车天地关于某品牌汽车的使用年限![]() (年)和所支出的维修费用
(年)和所支出的维修费用![]() (千元)由如表的统计资料:
(千元)由如表的统计资料:
| 2 | 3 | 4 | 5 | 6 |
| 2.1 | 3.4 | 5.9 | 6.6 | 7.0 |
(1)画出散点图并判断使用年限与所支出的维修费用是否线性相关;如果线性相关,求回归直线方程;
(2)若使用超过8年,维修费用超过1.5万元时,车主将处理掉该车,估计第10年年底时,车主是否会处理掉该车?
(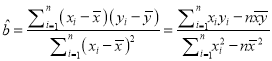 )
)