题目内容
12.已知1+$\sqrt{3}$tan10°=$\frac{1}{cosθ}$,且θ为锐角,则θ=40°.分析 先化切为弦,再通分,然后利用正弦加法定理和倍角公式能求出结果.
解答 解:∵1+$\sqrt{3}$tan10°=$\frac{1}{cosθ}$,且θ为锐角,
∴1+$\sqrt{3}tan10°$
=1+$\sqrt{3}$•$\frac{sin10°}{cos10°}$
=$\frac{cos10°+\sqrt{3}sin10°}{cos10°}$
=$\frac{2(\frac{\sqrt{3}}{2}sin10°+\frac{1}{2}cos10°)}{cos10°}$
=$\frac{2sin(10°+30°)}{cos10°}$
=$\frac{2sin40°}{cos10°}$
=$\frac{2sin40°}{sin80°}$
=$\frac{2sin40°}{2sin40°cos40°}$
=$\frac{1}{cos40°}$,
∴θ=40°.
故答案为:40°.
点评 本题考查三角函数值的求法,是中档题,解题时要认真审题,注意正弦加法定理和倍角公式的合理运用.

练习册系列答案
相关题目
2.$\frac{sin20°cos20°}{cos50°}$=( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
17.函数y=|cosx+$\frac{1}{2}$|的周期为( )
| A. | 2π | B. | π | C. | $\frac{π}{2}$ | D. | 4π |
4.已知α,β∈(0,$\frac{π}{2}$),且cosα=$\frac{4}{5}$,cos(α+β)=-$\frac{4}{5}$,则cosβ等于( )
| A. | $\frac{4}{25}$ | B. | $-\frac{4}{25}$ | C. | $\frac{7}{25}$ | D. | $-\frac{7}{25}$ |
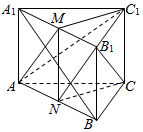 如图,正三棱柱ABC-A1B1C1的底面边长为2,AC1⊥A1B,M是A1B1的中点,N是AB中点,求证:
如图,正三棱柱ABC-A1B1C1的底面边长为2,AC1⊥A1B,M是A1B1的中点,N是AB中点,求证: