题目内容
19.已知抛物线C:y2=4x的焦点为F,过点F且倾斜角为$\frac{π}{3}$的直线与抛物线C相交于P,Q两点,则弦PQ的长为( )| A. | 3 | B. | 4 | C. | 5 | D. | $\frac{16}{3}$ |
分析 直线PQ的方程是$y=\sqrt{3}({x-1})$,把$y=\sqrt{3}({x-1})$代入抛物线y2=4x消y得3x2-10x+3=0,利用弦长公式,即可得出结论.
解答 解:直线PQ的方程是$y=\sqrt{3}({x-1})$,把$y=\sqrt{3}({x-1})$代入抛物线y2=4x消y得3x2-10x+3=0,
设Q(x1,y1),P(x2,y2),则${x_1}+{x_2}=\frac{10}{3}$,
所以|PQ|=x1+x2+p=$\frac{10}{3}+2$=$\frac{16}{3}$,
故选D.
点评 本题考查直线与抛物线位置关系的运用,考查弦长公式,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.已知非零向量$\overrightarrow{OA},\overrightarrow{OB}$不共线,且$2\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$,若$\overrightarrow{PA}=λ\overrightarrow{AB}(λ∈R)$,则x,y满足的关系是( )
| A. | x+y-2=0 | B. | 2x+y-1=0 | C. | x+2y-2=0 | D. | 2x+y-2=0 |
7.已知cos(θ+$\frac{π}{2}$)=$\frac{4}{5}$,-$\frac{π}{2}$<θ<$\frac{π}{2}$,则sin2θ的值等于( )
| A. | -$\frac{24}{25}$ | B. | $\frac{24}{25}$ | C. | -$\frac{12}{25}$ | D. | $\frac{12}{25}$ |
4.若数列{an}满足(2n+3)an+1-(2n+5)an=(2n+3)(2n+5)lg(1+$\frac{1}{n}$),且a1=5,则数列{$\frac{{a}_{n}}{2n+3}$}的第2016项为( )
| A. | lg2017 | B. | lg2016 | C. | 1+lg2016 | D. | 1+lg2017 |
8.有一段演绎推理:“直线平行于平面,则这条直线平行于平面内所有直线;已知直线b?平面α,直线a?平面α,直线b∥平面α,则直线b∥直线a”的结论是错误的,这是因为( )
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 非以上错误 |
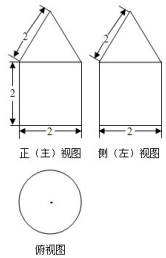 一个几何体的三视图如图所示:
一个几何体的三视图如图所示: