题目内容
19.已知非零向量$\overrightarrow{OA},\overrightarrow{OB}$不共线,且$2\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$,若$\overrightarrow{PA}=λ\overrightarrow{AB}(λ∈R)$,则x,y满足的关系是( )| A. | x+y-2=0 | B. | 2x+y-1=0 | C. | x+2y-2=0 | D. | 2x+y-2=0 |
分析 由于$\overrightarrow{PA}=λ\overrightarrow{AB}(λ∈R)$,即有$\overrightarrow{OA}$-$\overrightarrow{OP}$=λ($\overrightarrow{OB}$-$\overrightarrow{OA}$),可得$\overrightarrow{OP}$=(1+λ)$\overrightarrow{OA}$-λ$\overrightarrow{OB}$,又$2\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$,由于非零向量$\overrightarrow{OA},\overrightarrow{OB}$不共线,即可得到x,y满足的关系.
解答 解:由于$\overrightarrow{PA}=λ\overrightarrow{AB}(λ∈R)$,即有$\overrightarrow{OA}$-$\overrightarrow{OP}$=λ($\overrightarrow{OB}$-$\overrightarrow{OA}$),
∴$\overrightarrow{OP}$=(1+λ)$\overrightarrow{OA}$-λ$\overrightarrow{OB}$,
又$2\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$,由于非零向量$\overrightarrow{OA},\overrightarrow{OB}$不共线
则有$\frac{x+y}{2}$=1,可得x+y-2=0.
故选A.
点评 本题考查平面向量的运用,考查向量的加减运算以及不共线向量的性质,考查运算能力,属于中档题.

| A. | 1+2i | B. | -1+2i | C. | 1-2i | D. | -1-2i |
| A. | (-$\frac{1}{2}$,0) | B. | (-$\frac{1}{2}$,-$\frac{1}{4}$) | C. | ($\frac{1}{4}$,1) | D. | (-$\frac{1}{2}$,$\frac{1}{4}$) |
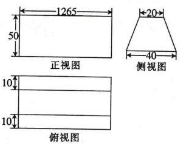 中国古代数学名著《九章算术》卷第五“商功”共收录28个题目,其中一个题目如下:今有城下广四丈,上广二丈,高五丈,袤一百二十六丈五尺,问积几何?其译文可用三视图来解释:某几何体的三视图如图所示(其中侧视图为等腰梯形,长度单位为尺),则该几何体的体积为( )
中国古代数学名著《九章算术》卷第五“商功”共收录28个题目,其中一个题目如下:今有城下广四丈,上广二丈,高五丈,袤一百二十六丈五尺,问积几何?其译文可用三视图来解释:某几何体的三视图如图所示(其中侧视图为等腰梯形,长度单位为尺),则该几何体的体积为( )| A. | 3795000立方尺 | B. | 2024000立方尺 | C. | 632500立方尺 | D. | 1897500立方尺 |
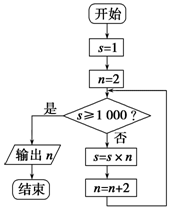
| A. | 输出使1×2×4×…×n≥1 000成立的最大整数n+2 | |
| B. | 输出使1×2×4×…×n≥1 000成立的最小整数n+2 | |
| C. | 输出使1×2×4×…×n≥1 000成立的最小整数n | |
| D. | 输出使1×2×4×…×n≥1 000成立的最大整数n |
| A. | 3 | B. | 4 | C. | 5 | D. | $\frac{16}{3}$ |
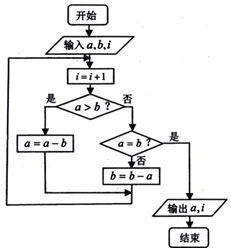 如图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为6,8,0 时,则输出的i=( )
如图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为6,8,0 时,则输出的i=( )