题目内容
(3)函数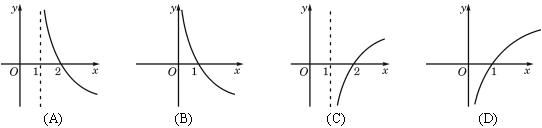
A
解析:∵0<a<1 y=1+ax单调递减
故其反函数相应区间上单调递减
∴排除C、D.
又∵ax>0 ∴y=1+ax>1 即反函数定义域为(1,+∞)

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
题目内容
(3)函数
A
解析:∵0<a<1 y=1+ax单调递减
故其反函数相应区间上单调递减
∴排除C、D.
又∵ax>0 ∴y=1+ax>1 即反函数定义域为(1,+∞)

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案