题目内容
如图,![]() 为矩形,
为矩形,![]() 为梯形,平面
为梯形,平面![]()
![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)若![]() 为
为![]() 中点,求证:
中点,求证:![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与
与![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
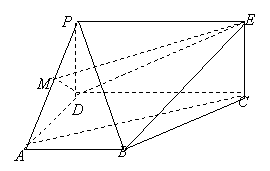 |
(Ⅰ) 证明:连结![]() ,交
,交![]() 与
与![]() ,连结
,连结![]() ,
,![]() 中,
中,![]() 分别为两腰
分别为两腰![]() 的中点 ∴
的中点 ∴![]() …………2分
…………2分
因为![]() 面
面![]() ,又
,又![]() 面
面![]() ,所以
,所以![]() 平面
平面![]() …………4分
…………4分
(Ⅱ) 设平面![]() 与
与![]() 所成锐二面角的大小为
所成锐二面角的大小为![]() ,以
,以![]() 为空间坐标系的原点,分别以
为空间坐标系的原点,分别以![]() 所在直线为
所在直线为![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
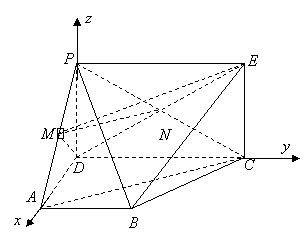
则![]()
![]() ……6分
……6分
设平面![]() 的单位法向量为
的单位法向量为![]() ,
,
则可设![]() …………7分
…………7分
设面![]() 的法向量
的法向量![]() ,应有
,应有
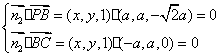
即: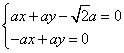 ,解得:
,解得: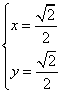 ,所以
,所以![]() …………10分
…………10分
∴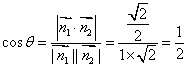 …………11分
…………11分
所以平面![]() 与
与![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() …………12分
…………12分

练习册系列答案
相关题目
 如图,现有一块半径为2m,圆心角为90°的扇形铁皮AOB,欲从其中裁剪出一块内接五边形
如图,现有一块半径为2m,圆心角为90°的扇形铁皮AOB,欲从其中裁剪出一块内接五边形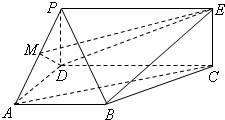 如图PDCE为矩形,ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=
如图PDCE为矩形,ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD= 为矩形,
为矩形, 为梯形,平面
为梯形,平面 平面
平面 ,
, ,
, .
.
 为
为 中点,求证:
中点,求证: 平面
平面 ;
; 与
与 所成锐二面角的余弦值.
所成锐二面角的余弦值. (本小题满分12分)如图,
(本小题满分12分)如图,