题目内容
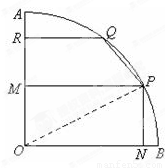
 如图,现有一块半径为2m,圆心角为90°的扇形铁皮AOB,欲从其中裁剪出一块内接五边形
如图,现有一块半径为2m,圆心角为90°的扇形铁皮AOB,欲从其中裁剪出一块内接五边形ONPQR,使点P在AB弧上,点M,N分别在半径OA和OB上,四边形PMON是矩形,点Q在弧AP上,R点在线段AM上,四边形PQRM是直角梯形.现有如下裁剪方案:先使矩形PMON的面积达到最大,在此前提下,再使直角梯形PQRM的面积也达到最大.
(Ⅰ)设∠BOP=θ,当矩形PMON的面积最大时,求θ的值;
(Ⅱ)求按这种裁剪方法的原材料利用率.
分析:(Ⅰ)设∠BOP=θ,θ∈(0,
),则PM=2cosθ,PN=2sinθ,从而SPMON=PM•PN=2sin2θ,由此可求当矩形PMON的面积最大时,θ的值;
(Ⅱ)过Q点作QS⊥OB,垂足为S,连接OQ,设∠BOQ=α,α∈(
,
),从而可得S梯形PQRM=
(2cosα+
)(2sinα-
)=2sinαcosα+
(sinα-cosα)-1,利用换元法t=sinα-cosα=
sin(α-
),可得S梯形PQRM=-t2 +
t=-(t-
)2+
,从而可求直角梯形PQRM的面积的最大值,由此可求原材料利用率.
| π |
| 2 |
(Ⅱ)过Q点作QS⊥OB,垂足为S,连接OQ,设∠BOQ=α,α∈(
| π |
| 4 |
| π |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| π |
| 4 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
解答:解:(Ⅰ)先求矩形PMON面积的最大值:
设∠BOP=θ,θ∈(0,
),则PM=2cosθ,PN=2sinθ,
∴SPMON=PM•PN=2sin2θ,
∴当2θ=
,即θ=
时,Smax=2
此时,PM=MO=
,θ=
…6分
(Ⅱ)过Q点作QS⊥OB,垂足为S,连接OQ,设∠BOQ=α,α∈(
,
)
在Rt△QOS中,有QS=2sinα,OS=2cosα,
则RQ=2cosα,RM=2sinα-
,
∴S梯形PQRM=
(2cosα+
)(2sinα-
)=2sinαcosα+
(sinα-cosα)-1 …8分
令t=sinα-cosα=
sin(α-
),
∵α∈(
,
),∴t∈(0,1),
此时,2sinαcosα=1-t2,则S梯形PQRM=-t2 +
t=-(t-
)2+
,
当t=
时,直角梯形PQRM的面积的最大值为
…10分
∴方案裁剪出内接五边形ONPQR的面积最大值为
m2,即利用率=
=
…12分.
设∠BOP=θ,θ∈(0,
| π |
| 2 |
∴SPMON=PM•PN=2sin2θ,
∴当2θ=
| π |
| 2 |
| π |
| 4 |
此时,PM=MO=
| 2 |
| π |
| 4 |
(Ⅱ)过Q点作QS⊥OB,垂足为S,连接OQ,设∠BOQ=α,α∈(
| π |
| 4 |
| π |
| 2 |
在Rt△QOS中,有QS=2sinα,OS=2cosα,
则RQ=2cosα,RM=2sinα-
| 2 |
∴S梯形PQRM=
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
令t=sinα-cosα=
| 2 |
| π |
| 4 |
∵α∈(
| π |
| 4 |
| π |
| 2 |
此时,2sinαcosα=1-t2,则S梯形PQRM=-t2 +
| 2 |
| ||
| 2 |
| 1 |
| 2 |
当t=
| ||
| 2 |
| 1 |
| 2 |
∴方案裁剪出内接五边形ONPQR的面积最大值为
| 5 |
| 2 |
2+
| ||
| π |
| 5 |
| 2π |
点评:本题考查利用三角知识解决实际问题,解题的关键是引入辅助角,构建三角函数模型,利用三角函数知识进行解决,综合性强.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
 的扇形铁皮
的扇形铁皮 ,欲从其中裁剪出一块内接五边形
,欲从其中裁剪出一块内接五边形 ,使点
,使点 在
在 弧上,点
弧上,点 分别在半径
分别在半径 和
和 上,四边形
上,四边形 是矩形,点
是矩形,点 在弧
在弧 上,
上, 点在线段
点在线段 上,四边形
上,四边形 是直角梯形.现有如下裁剪方案:先使矩形
是直角梯形.现有如下裁剪方案:先使矩形 ,当矩形
,当矩形 的值;
的值;
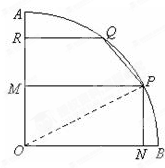 如图,现有一块半径为2m,圆心角为90°的扇形铁皮AOB,欲从其中裁剪出一块内接五边形
如图,现有一块半径为2m,圆心角为90°的扇形铁皮AOB,欲从其中裁剪出一块内接五边形