题目内容
O、A、B、C为空间四个点，又
、
、
为空间的一个基底，则( )A.O、A、B、C四点不共线
B.O、A、B、C四点共面，但不共线
C.O、A、B、C四点中任三点不共线
D.O、A、B、C四点不共面
解析：由基底意义,、、三个向量不共面, 但A、B、C三种情形都有可能使
、
、
共面, 只有D才能使这三个向量不共面.
答案：D
练习册系列答案
相关题目
O、A、B、C为空间四边形四个顶点，点M、N分别是边OA、BC的中点，且
=
，
=
，
=
，用
，
，
表示向量
为（ ）
| OA |
| a |
| OB |
| b |
| OC |
| c |
| a |
| b |
| c |
| MN |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
有以下命题：
①如果向量
，
与任何向量不能构成空间向量的一组基底，那么
，
的关系是不共线；
②O，A，B，C为空间四点，且向量
，
，
不构成空间的一个基底，那么点O，A，B，C一定共面；
③已知向量
，
，
是空间的一个基底，则向量
+
，
-
，
，也是空间的一个基底．
其中正确的命题是（ ）
①如果向量
| a |
| b |
| a |
| b |
②O，A，B，C为空间四点，且向量
| OA |
| OB |
| OC |
③已知向量
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| c |
其中正确的命题是（ ）
| A、①② | B、①③ | C、②③ | D、①②③ |
已知点O、A、B、C为空间不共面的四点，且向量
=
+
+
，向量
=
+
-
，则与
、
不能构成空间基底的向量是（ ）
| a |
| OA |
| OB |
| OC |
| b |
| OA |
| OB |
| OC |
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
、
、
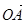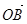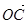为空间的一个基底，则（ ）