题目内容
有4个命题:
①O,A,B,C为空间四点,且
,
,
不构成空间的一个基底,那么点O,A,B,C一定共面
②若
与
共线,
与
共线,则
与
共线
③若
与
,
共面,则
=x
+y
④若
=x
+y
,则P,M,A,B共面
其中,真命题的个数是( )
①O,A,B,C为空间四点,且
| OA |
| OB |
| OC |
②若
| a |
| b |
| b |
| c |
| a |
| c |
③若
| p |
| a |
| b |
| p |
| a |
| b |
④若
| MP |
| MA |
| MB |
其中,真命题的个数是( )
分析:本题综合考查了共线向量与向量共线定理,以及向量共面定理与点共面的共线,我们要根据向量共线、共面的定义和性质对四个命题逐一进行判断,即可得到答案.
解答:解:①O,A,B,C为空间四点,且向量
,
,
不构成空间的一个基底,那么点O,A,B,C一定共面;这是正确的.
②如果
=
,则
与
不一定共线,所以②错误;
③不正确,如
,
都是零向量,而
为非零向量时,此等式不成立.
④若
=x
+y
,则
,
,
共面,故四点 P、M、A、B共面,故④正确.
所以①④正确.
故选B.
| OA |
| OB |
| OC |
②如果
| b |
| 0 |
| a |
| c |
③不正确,如
| a |
| b |
| p |
④若
| MP |
| MA |
| MB |
| MP |
| MA |
| MB |
所以①④正确.
故选B.
点评:本题考查平面向量基本定理的应用,注意特殊情况,通过给变量取特殊值,举反例来说明某个命题不正确,是一种简单有效的方法.

练习册系列答案
相关题目
 10、如图,平面中两条直线l1和l2相交于点O,对于平面上任意一点M,若p、q分别是M到直线l1和l2的距离,则称有序非负实数对(p,q)是点M的“距离坐标”.已知常数p≥0,q≥0,给出下列命题:
10、如图,平面中两条直线l1和l2相交于点O,对于平面上任意一点M,若p、q分别是M到直线l1和l2的距离,则称有序非负实数对(p,q)是点M的“距离坐标”.已知常数p≥0,q≥0,给出下列命题: 给出下列5个命题:
给出下列5个命题: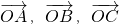 不构成空间的一个基底,那么点O,A,B,C一定共面
不构成空间的一个基底,那么点O,A,B,C一定共面 与
与 共线,
共线, 共线,则
共线,则 与
与 共面,则
共面,则
 ,则P,M,A,B共面
,则P,M,A,B共面 不构成空间的一个基底,那么点O,A,B,C一定共面
不构成空间的一个基底,那么点O,A,B,C一定共面 与
与 共线,
共线, 与
与 共线,则
共线,则 与
与 共线
共线 与
与 共面,则
共面,则
 ,则P,M,A,B共面
,则P,M,A,B共面