题目内容
O、A、B、C为空间四边形四个顶点,点M、N分别是边OA、BC的中点,且
=
,
=
,
=
,用
,
,
表示向量
为( )
| OA |
| a |
| OB |
| b |
| OC |
| c |
| a |
| b |
| c |
| MN |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
分析:由题意,O、A、B、C为空间四边形四个顶点,点M、N分别是边OA、BC的中点,由用向量的加法法则可以得出
=
+
+
,根据图形用
,
,
表示出再对照四个选项得出正确答案
| MN |
| MA |
| AB |
| BN |
| a |
| b |
| c |
解答: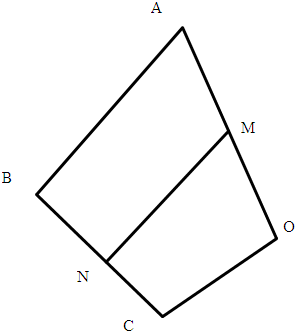 解:如图
解:如图
=
+
+
又点M、N分别是边OA、BC的中点
∴
=
+
+
=
+
+
=
+
-
+
=
+
-
+
×(
-
)
=-
+
+
又
=
,
=
,
=
,
∴
=
(
+
-
)
故选C
 解:如图
解:如图| MN |
| MA |
| AB |
| BN |
又点M、N分别是边OA、BC的中点
∴
| MN |
| MA |
| AB |
| BN |
=
| 1 |
| 2 |
| OA |
| AB |
| BN |
=
| 1 |
| 2 |
| OA |
| OB |
| OA |
| 1 |
| 2 |
| BC |
=
| 1 |
| 2 |
| OA |
| OB |
| OA |
| 1 |
| 2 |
| OC |
| OB |
=-
| 1 |
| 2 |
| OA |
| 1 |
| 2 |
| OB |
| 1 |
| 2 |
| OC |
又
| OA |
| a |
| OB |
| b |
| OC |
| c |
∴
| MN |
| 1 |
| 2 |
| c |
| b |
| a |
故选C
点评:本题考查向量的加减运算及其几何意义,解题的关键是作出图象由向量的线性运算规则用三个向量表示出向量
| MN |

练习册系列答案
相关题目
有以下命题:
①如果向量
,
与任何向量不能构成空间向量的一组基底,那么
,
的关系是不共线;
②O,A,B,C为空间四点,且向量
,
,
不构成空间的一个基底,那么点O,A,B,C一定共面;
③已知向量
,
,
是空间的一个基底,则向量
+
,
-
,
,也是空间的一个基底.
其中正确的命题是( )
①如果向量
| a |
| b |
| a |
| b |
②O,A,B,C为空间四点,且向量
| OA |
| OB |
| OC |
③已知向量
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| c |
其中正确的命题是( )
| A、①② | B、①③ | C、②③ | D、①②③ |
已知点O、A、B、C为空间不共面的四点,且向量
=
+
+
,向量
=
+
-
,则与
、
不能构成空间基底的向量是( )
| a |
| OA |
| OB |
| OC |
| b |
| OA |
| OB |
| OC |
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
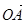 、
、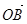 、
、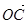 为空间的一个基底,则( )
为空间的一个基底,则( )