题目内容
11.下列函数y=x${\;}^{\frac{1}{5}}$,y=x${\;}^{\frac{1}{4}}$,y=x${\;}^{-\frac{2}{3}}$,y=x${\;}^{-\frac{1}{2}}$中,定义域为{x∈R|x>0}的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据题意,分别写出这四个函数的定义域,即可得出所以符合条件的函数有几个.
解答 解:函数y=x${\;}^{\frac{1}{5}}$的定义域为R,
函数y=x${\;}^{\frac{1}{4}}$的定义域为{x|x≥0};
函数y=x${\;}^{-\frac{2}{3}}$的定义域为{x|x≠0};
函数y=x${\;}^{-\frac{1}{2}}$中的定义域为{x∈R|x>0};
所以符合条件的函数只有1个.
故选:A.
点评 本题考查了求常见的函数定义域的应用问题,是基础题目.

练习册系列答案
相关题目
20.函数y=$\frac{x+2}{x-1}$(x≠1)在区间[2,5)上的最大值、最小值分别是( )
| A. | $\frac{7}{4}$,4 | B. | 无最大值,最小值7 | ||
| C. | 4,0 | D. | 最大值4,无最小值 |
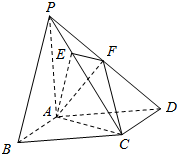 如图,四棱锥P-ABCD的底面ABCD是正方形,PA⊥平面ABCD,AP=AD=1,点E在PC上,且PE=$\frac{1}{2}$EC,点F是PD的中点.
如图,四棱锥P-ABCD的底面ABCD是正方形,PA⊥平面ABCD,AP=AD=1,点E在PC上,且PE=$\frac{1}{2}$EC,点F是PD的中点.