题目内容
1.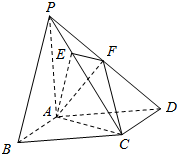 如图,四棱锥P-ABCD的底面ABCD是正方形,PA⊥平面ABCD,AP=AD=1,点E在PC上,且PE=$\frac{1}{2}$EC,点F是PD的中点.
如图,四棱锥P-ABCD的底面ABCD是正方形,PA⊥平面ABCD,AP=AD=1,点E在PC上,且PE=$\frac{1}{2}$EC,点F是PD的中点.(1)求证:PC⊥AF;
(2)求三棱锥A-CEF的体积.
分析 (1)要证PC⊥AF,因为PC?面PCD,可证AF⊥面PCD,由已知底面ABCD是正方形,PA⊥平面ABCD,易得AF⊥CD,再由PA=AD,点F是棱PD的中点得到AF⊥PD,则问题得证;
(2)转换底面,求三棱锥A-CEF的体积.
解答  (1)证明:∵PA⊥平面ABCD,CD?平面ABCD
(1)证明:∵PA⊥平面ABCD,CD?平面ABCD
又ABCD是矩形,∴CD⊥AD,
∵PA∩AD=A,∴CD⊥平面PAD.
∵AF?平面PAD,∴AF⊥CD.
∵PA=AD,点F是PD的中点,∴AF⊥PD.
又CD∩PD=D,∴AF⊥平面PDC.
∵PC?平面PDC,∴PC⊥AF;
(2)解:连接BD,则BD⊥AC,
∵BD⊥PA,PA∩AC=A,
∴BD⊥平面PAC,
∴D到平面PAC的距离为$\frac{\sqrt{2}}{2}$,
∵点F是PD的中点,
∴F到平面PAC的距离为$\frac{\sqrt{2}}{4}$.
∵点E在PC上,且PE=$\frac{1}{2}$EC,
∴S△EAC=$\frac{1}{2}×\sqrt{2}×\frac{2}{3}$=$\frac{\sqrt{2}}{3}$,
∴三棱锥A-CEF的体积V=VF-EAC=$\frac{1}{3}×\frac{\sqrt{2}}{3}×\frac{\sqrt{2}}{4}$=$\frac{1}{18}$.
点评 本题考查了由线面垂直得线线垂直,考查了三棱锥A-CEF的体积,综合考查了学生的空间想象能力和思维能力,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.偶函数f(x)的定义域为R,若f(x+2)为奇函数,且f(1)=1,则f(89)+f(90)为( )
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
9.若f(x)=$\frac{{e}^{x}-{e}^{-x}}{2}$,g(x)=$\frac{{e}^{x}+{e}^{-x}}{2}$,则f(2x)等于( )
| A. | 2f(x) | B. | 2[f(x)+g(x)] | C. | 2g(x) | D. | 2f(x)•g(x) |
13.已知F1,F2分别是双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左、右焦点,O为坐标原点,P为双曲线右支上的一点,PF1与以F2为圆心,|OF2|为半径的圆相切于点Q,且Q恰好是PF1的中点,则双曲线C的离心率为( )
| A. | $\frac{{\sqrt{3}+1}}{2}$ | B. | $\sqrt{3}+1$ | C. | $\frac{{\sqrt{6}}}{2}$ | D. | $\sqrt{5}-1$ |
 如图,在四边形ABCB′,△ABC≌△AB′C,AB⊥AB′,cos∠BCB′=$\frac{3}{4}$,BC=2$\sqrt{2}$.
如图,在四边形ABCB′,△ABC≌△AB′C,AB⊥AB′,cos∠BCB′=$\frac{3}{4}$,BC=2$\sqrt{2}$.