题目内容
12.函数$y=\frac{{1+{2^x}}}{{1+{4^x}}}$的值域为( )| A. | $({0,\frac{{\sqrt{2}+1}}{2}}]$ | B. | $({-∞,\frac{{\sqrt{2}+1}}{2}}]$ | C. | (-∞,0] | D. | (-∞,1] |
分析 令2x=t(t>0),则$y=\frac{{1+{2^x}}}{{1+{4^x}}}$=$\frac{1+t}{1+{t}^{2}}$,然后利用导数求得函数的值域.
解答 解:令2x=t(t>0),
则$y=\frac{{1+{2^x}}}{{1+{4^x}}}$=$\frac{1+t}{1+{t}^{2}}$,
∴y′=$\frac{1+{t}^{2}-2t(1+t)}{(1+{t}^{2})^{2}}=\frac{1-2t-{t}^{2}}{(1+{t}^{2})^{2}}$,
由y′=0,得t=-1$-\sqrt{2}$(舍)或t=-1+$\sqrt{2}$.
∴当t∈(0,-1+$\sqrt{2}$)时,y′>0,当t∈(-1+$\sqrt{2}$,+∞)时,y′<0,
∴y=$\frac{1+t}{1+{t}^{2}}$在(0,-1+$\sqrt{2}$)上为增函数,在(-1+$\sqrt{2}$,+∞)上为减函数.
∴当t=-1+$\sqrt{2}$时,y有最大值为$\frac{1-1+\sqrt{2}}{1+(-1+\sqrt{2})^{2}}=\frac{\sqrt{2}+1}{2}$.
又当t→0+时,y→1,当t→+∞时,y→0.
∴$y=\frac{{1+{2^x}}}{{1+{4^x}}}$=$\frac{1+t}{1+{t}^{2}}$的值域为(0,$\frac{\sqrt{2}+1}{2}$].
故选:A.
点评 本题考查利用换元法及导数求函数的最值,考查利用导数研究函数的单调性,是中档题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案
相关题目
16.甲、乙、丙、丁四位同学一起去问老师询问成语竞赛的成绩.老师说:你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩.根据以上信息,则( )
| A. | 乙可以知道四人的成绩 | B. | 丁可以知道四人的成绩 | ||
| C. | 乙、丁可以知道对方的成绩 | D. | 乙、丁可以知道自己的成绩 |
4.已知函数f(x)=sin(ωx+φ)(φ>0,-π<φ<0)的最小正周期是π,将f(x)图象向左平移$\frac{π}{3}$个单位长度后,所得的函数图象过点P(0,1),则函数f(x)( )
| A. | 在区间[-$\frac{π}{6}$,$\frac{π}{3}$]上单调递减 | B. | 在区间[-$\frac{π}{6}$,$\frac{π}{3}$]上单调递增 | ||
| C. | 在区间[-$\frac{π}{3}$,$\frac{π}{6}$]上单调递减 | D. | 在区间[-$\frac{π}{3}$,$\frac{π}{6}$]上单调递增 |
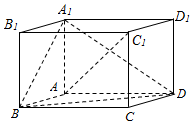 如图,在平行六面体ABCD-A1B1C1D1中,AA1⊥平面ABCD,且AB=AD=2,AA1=$\sqrt{3}$,∠BAD=120°.
如图,在平行六面体ABCD-A1B1C1D1中,AA1⊥平面ABCD,且AB=AD=2,AA1=$\sqrt{3}$,∠BAD=120°.