题目内容
4.设过函数f(x)=lnx+x的图象上任意一点处的切线为l1,总存在过函数g(x)=2x+acosx的图象上一点处的切线l2,使得l1⊥l2,则实数a的取值范围是( )| A. | [-1,2] | B. | (-∞,-3]∪[3,+∞) | C. | (-∞,-1]∪(2,+∞) | D. | (-∞,-1)∪[2,+∞) |
分析 求得f(x)的导数,可得切线l1的斜率k1,求得g(x)的导数,可得切线l2的斜率k2,运用两直线垂直的条件:斜率之积为-1,结合正弦函数的值域和条件可得(-1,0)⊆[2-|a|,2+|a|],得到不等式组,解得a的范围即可.
解答 解:∵函数f(x)=lnx+x,∴f′(x)=$\frac{1}{x}+1$,x>0,
∴过函数f(x)=lnx+x的图象上任意一点处的切线l1的斜率k1=$\frac{1}{{x}_{1}}+1$,
∵g(x)=2x+acosx,∴g′(x)=2-asinx,
∵过函数f(x)=lnx+x的图象上任意一点处的切线为l1,
总存在过函数g(x)=2x+acosx的图象上一点处的切线l2,
∴切线l2的斜率k2=2-asinx2,
∵l1⊥l2,∴k1k2=($\frac{1}{{x}_{1}}$+1)(2-asinx2)=-1,
∴2-asinx2=-$\frac{{x}_{1}}{{x}_{1}+1}$=-1+$\frac{1}{{x}_{1}+1}$,
∵x1>0,∴-$\frac{{x}_{1}}{{x}_{1}+1}$∈(-1,0),
2-asinx2∈[2-|a|,2+|a|],
∵?x1,?x2使得等式成立,
∴(-1,0)⊆[2-|a|,2+|a|],
∴$\left\{\begin{array}{l}{2-|a|≤-1}\\{2+|a|≥0}\end{array}\right.$,故|a|≥3,
解得:a≥3或a≤-3,
故选:B.
点评 本题考查导数的应用:求切线的斜率,考查两直线垂直的条件:斜率之积为-1,以及转化思想的运用,区间的包含关系,考查运算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.若函数y=f(x)同时具有下列三个性质:(1)最小正周期为π;(2)在$x=\frac{π}{3}$时取得最大值1;(3)在区间$[{-\frac{π}{6},\frac{π}{3}}]$上是增函数.则y=f(x)的解析式可以是( )
| A. | $y=sin({\frac{x}{2}+\frac{π}{6}})$ | B. | $y=cos({2x+\frac{π}{3}})$ | C. | $y=sin({2x-\frac{π}{6}})$ | D. | $y=cos({2x-\frac{π}{6}})$ |
14.设a、b∈R,则“a3>b3且ab<0”是“$\frac{1}{a}$>$\frac{1}{b}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 ,
, ,则
,则 等于( )
等于( ) B.
B.
 D.
D.
 中,若
中,若 ,
, ,
, ,则
,则 ( )
( ) B.
B.
 D.
D.
 的定义域为
的定义域为 ,则实数
,则实数 的取值范围是( )
的取值范围是( )



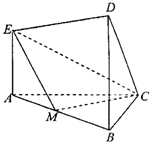 在如图所示的几何体中.EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M是AB的中点.
在如图所示的几何体中.EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M是AB的中点.