题目内容
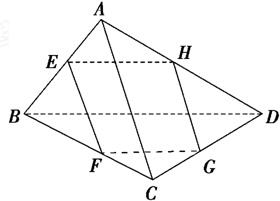 如图所示,空间四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA上的点,请回答下列问题:
如图所示,空间四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA上的点,请回答下列问题:(1)满足什么条件时,四边形EFGH为平行四边形?
(2)满足什么条件时,四边形EFGH为矩形?
(3)满足什么条件时,四边形EFGH为正方形?
分析:(1)E,F,G,H分别为所在边的中点,说明四边形EFGH为平行四边形,利用类比推理相似比判断得到结果;
(2)E,F,G,H分别为所在边的中点且BD⊥AC,判定四边形EFGH为矩形;
(3)E,F,G,H分别为所在边的中点且BD⊥AC,AC=BD,判定四边形EFGH为正方形.
(2)E,F,G,H分别为所在边的中点且BD⊥AC,判定四边形EFGH为矩形;
(3)E,F,G,H分别为所在边的中点且BD⊥AC,AC=BD,判定四边形EFGH为正方形.
解答:解:(1)当E,F,G,H满足
=
=
=
时,四边形EFGH为平行四边形,
不妨以E,F,G,H分别为所在边的中点,证明如下:
∵E,H分别是AB,AD的中点,
∴EH
BD,同理,FG
BD.
从而EH綊FG,所以四边形EFGH为平行四边形.
(2)当E,F,G,H分别为所在边的中点且BD⊥AC时,可得AC∥EF,BD∥FG,所以EF⊥FG,所以平行四边形EFGH为矩形.
(3)当E,F,G,H分别为所在边的中点且BD⊥AC,可得AC∥EF,BD∥FG,所以EF⊥FG,所以平行四边形EFGH为矩形,AC=BD时
EF=FG,四边形EFGH为正方形.
| BE |
| BA |
| BF |
| BC |
| DH |
| DA |
| DG |
| DC |
不妨以E,F,G,H分别为所在边的中点,证明如下:
∵E,H分别是AB,AD的中点,
∴EH
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
| 1 |
| 2 |
从而EH綊FG,所以四边形EFGH为平行四边形.
(2)当E,F,G,H分别为所在边的中点且BD⊥AC时,可得AC∥EF,BD∥FG,所以EF⊥FG,所以平行四边形EFGH为矩形.
(3)当E,F,G,H分别为所在边的中点且BD⊥AC,可得AC∥EF,BD∥FG,所以EF⊥FG,所以平行四边形EFGH为矩形,AC=BD时
EF=FG,四边形EFGH为正方形.
点评:本题考查棱锥的结构特征及其性质,考查基本知识掌握情况,是基础题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
 如图所示,空间四边形ABCD中,AB=BD=AD=2,BC=CD=
如图所示,空间四边形ABCD中,AB=BD=AD=2,BC=CD=
| ||
| 2 |
| 3 |
| 2 |
| A、30° | B、45° |
| C、60° | D、90° |
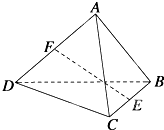 如图所示,空间四边形ABCD中,AB=CD,AB⊥CD,E、F分别为BC、AD的中点,则EF和AB所成的角为
如图所示,空间四边形ABCD中,AB=CD,AB⊥CD,E、F分别为BC、AD的中点,则EF和AB所成的角为
