题目内容
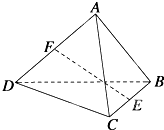如图所示，空间四边形ABCD中，AB=CD，AB⊥CD，E、F分别为BC、AD的中点，则EF和AB所成的角为45°
45°
．分析：先作出异面直线所成的角，再在三角形中求解．
解答：
解：取AC的中点M，连接EM、FM．
∵E为BC的中点，∴EM∥AB且EM=
AB；
同理：FM∥CD且FM=
CD，
∴∠FEM为异面直线AB、EF所成的角，
又∵AB⊥CD，AB=CD，∴FM=EM，FM⊥EM，
∴△EFM为等腰直角三角形，∴∠FEM=45°
故答案是45°．
解：取AC的中点M，连接EM、FM．∵E为BC的中点，∴EM∥AB且EM=
| 1 |
| 2 |
同理：FM∥CD且FM=
| 1 |
| 2 |
∴∠FEM为异面直线AB、EF所成的角，
又∵AB⊥CD，AB=CD，∴FM=EM，FM⊥EM，
∴△EFM为等腰直角三角形，∴∠FEM=45°
故答案是45°．
点评：本题考查异面直线所成的角的定义及求法．求异面直线所成的角的方法：1、作角（平行线）；2、证角（符合定义）；3、求角（解三角形）．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，空间四边形ABCD中，AB=BD=AD=2，BC=CD=
| ||
| 2 |
| 3 |
| 2 |
| A、30° | B、45° |
| C、60° | D、90° |
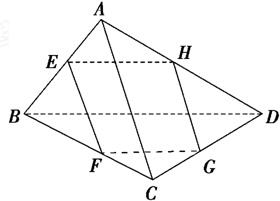如图所示，空间四边形ABCD中，E、F、G、H分别为AB、BC、CD、DA上的点，请回答下列问题：
