题目内容
如图所示，空间四边形ABCD中，AB=BD=AD=2，BC=CD=
| ||
| 2 |
| 3 |
| 2 |
| A、30° | B、45° |
| C、60° | D、90° |
分析：由题意得，FC是三角形BDE的中位线，可得∠AFC或其补角为所求，由余弦定理求得cos∠AFC 的值，进而得到
∠AFC，从而得到异面直线 AF、DE 所成角．
∠AFC，从而得到异面直线 AF、DE 所成角．
解答：解：由题意得，FC是三角形BDE的中位线，∴FC∥DE 且 FC=
DE，故∠AFC或其补角为所求．
等边三角形ABD中，AF=AB sin60°=
，FC=
=
=
，
由余弦定理可得
=3 +
-2×
×
cos∠AFC，∴cos∠AFC=
．
故∠AFC=60°，即异面直线 AF、DE 所成角为 60°，
故选 C．
| 1 |
| 2 |
等边三角形ABD中，AF=AB sin60°=
| 3 |
| BC2-BF2 |
(
|
| ||
| 2 |
由余弦定理可得
| 9 |
| 4 |
| 3 |
| 4 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
故∠AFC=60°，即异面直线 AF、DE 所成角为 60°，
故选 C．
点评：本题考查异面直线所成的角的定义和求法，找出异面直线所成的角是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
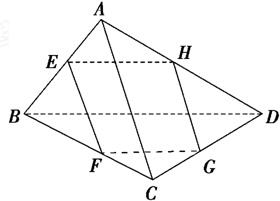如图所示，空间四边形ABCD中，E、F、G、H分别为AB、BC、CD、DA上的点，请回答下列问题：
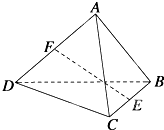如图所示，空间四边形ABCD中，AB=CD，AB⊥CD，E、F分别为BC、AD的中点，则EF和AB所成的角为
