题目内容
若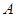
为不等式组
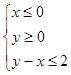表示的平面区域，当
从
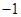连续变化到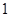
时，动直线
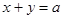扫过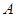中的那部分区域的面积为（ ）
A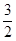． | B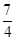． | C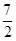． | D． |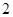
A
解析试题分析：作出可行域，如图，可知则直线扫过的面积为三角形面积的差得到，即为S=
,故选A.
考点：线性规划问题
点评：平面区域的面积问题是线性规划问题中一类重要题型，在解题时，关键是正确地画出平面区域，然后结合有关面积公式求解
练习册系列答案
优质课堂快乐成长系列答案
相关题目
设变量
满足约束条件
，则目标函数
的最大值和最小值分别为
A． | B． | C． | D． |
已知
满足
，则
的最小值为（ ）
| A．6 | B．8 | C．12 | D．15 |
已知变量x、y满足的约束条件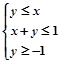
，则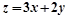
的最大值为( )
| A．-3 | B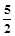． | C．-5 | D．4 |
已知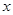
，
满足
, 且目标函数
的最大值为7，最小值为１，则
（ ）
| A．1 | B． | C．２ | D． |
设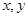
满足约束条件
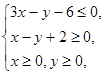若目标函数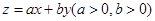
的值是最大值为12，则
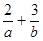的最小值为( ).
A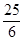． | B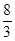． | C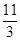． | D．4 |
的取值范围是
不等式组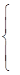 
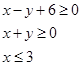，表示平面区域的面积为（ ）
| A．12 | B．18 | C． 32 | D．36 |
已知平面区域如右图所示，
在平面区域内取得最大值的最优解有无数多个，则
的值为 （ ）
A． | B． | C． | D．不存在 |