题目内容
随机变量ξ的概率分布列为P（ξ=n）=| a |
| n(n+1) |
| 2 |
| 3 |
| 7 |
| 3 |
分析：先根据分布列中所有的概率和为1求出参数a，再判断出满足
＜ξ＜
之间的ξ的值，代入分布列求出值．
| 2 |
| 3 |
| 7 |
| 3 |
解答：解：根据分布列中所有的概率和为1，得
+
+
+
=1
解得a=
∴P(ξ=n)=
∴P(
＜ξ＜
)=P（ξ=1）+P（ξ=2）=
+
=
故答案为
| a |
| 1×2 |
| a |
| 2×3 |
| a |
| 3×4 |
| a |
| 4×5 |
解得a=
| 5 |
| 4 |
∴P(ξ=n)=
| ||
| n(n+1) |
∴P(
| 2 |
| 3 |
| 7 |
| 3 |
| 5 |
| 8 |
| 5 |
| 24 |
| 5 |
| 6 |
故答案为
| 5 |
| 6 |
点评：解决随机变量的分布列问题，一定要注意分布列的特点，各个概率值在[0，1]之间；概率和为1；常与求随机变量的期望、方差一起出题，常出现在高考题中的解答题中．
练习册系列答案
相关题目
随机变量X的概率分布规律为P（X=n）=
（n=1，2，3，4），其中a是常数，则P（
＜X＜
）的值为（ ）
| a |
| n(n+1) |
| 1 |
| 2 |
| 5 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
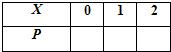从装有3个红球，2个白球的袋中随机取出2个球，设其中有X个红球，则随机变量X的概率分布为