Question

设f(x)=ax²+bx,且1≤f(-1)≤2,2≤?f(1)≤?4,求f(-2)的取值范围.

Answer 1

思路分析:严格根据不等式的基本性质和运算法则,将f(-2)用含f(-1)和f(1)的式子表示.

解:设f(-2)=mf(-1)+nf(1)(m,n为待定系数),??

则4a-2b=m(a-b)+n(a+b),即4a-2b=(m+n)a-(m-n)b,?

于是,得解得

∴f(-2)=3f(-1)+f(1).?

∵1≤f(-1)≤2,∴2≤f(1)≤4.?

∴5≤3f(-1)+f(1)≤10,故5≤f(-2)≤10.?

以上解题过程简化如下:?

由得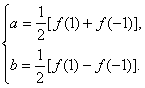

∴f(-2)=4a-2b=3f(-1)+f(1).

温馨提示

不等式的性质及其证明方法是学习不等式证明的基础,是本节的重点.