题目内容
已知数列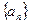 各项均为正数,
各项均为正数,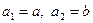 ,且对于正整数
,且对于正整数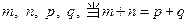 时,都有
时,都有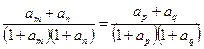 。
。
(I)当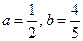 ,求
,求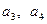 的值,并求数列
的值,并求数列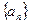 的通项公式;
的通项公式;
(II)证明:对于任意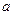 ,存在与
,存在与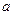 有关的常数
有关的常数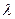 ,使得对于每个正整数
,使得对于每个正整数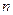 ,都有
,都有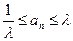 。
。
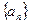 各项均为正数,
各项均为正数,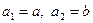 ,且对于正整数
,且对于正整数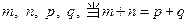 时,都有
时,都有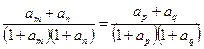 。
。(I)当
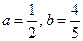 ,求
,求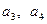 的值,并求数列
的值,并求数列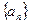 的通项公式;
的通项公式;(II)证明:对于任意
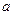 ,存在与
,存在与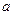 有关的常数
有关的常数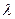 ,使得对于每个正整数
,使得对于每个正整数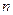 ,都有
,都有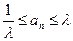 。
。解:(I)令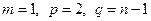 ,则
,则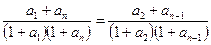
将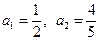 代入上式,得
代入上式,得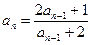 (*)
(*)
∴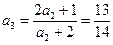 ,
,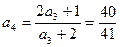 ,
,
且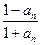
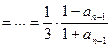 ,
,
故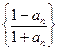 为等比数列,且
为等比数列,且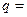
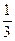 ,
,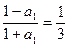
∴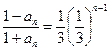 ,∴
,∴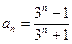 。
。
(II)由题设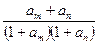 值仅与
值仅与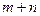 有关,设为
有关,设为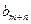 。
。
则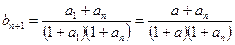 ,
,
考察函数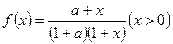 ,则在定义域上有
,则在定义域上有
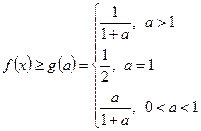
故对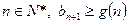 恒成立,又
恒成立,又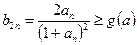 ,
,
注意到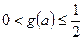 ,解上式得
,解上式得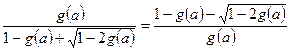
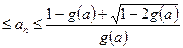 ,
,
取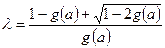 ,即有
,即有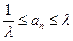 。
。
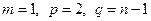 ,则
,则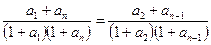
将
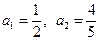 代入上式,得
代入上式,得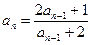 (*)
(*)∴
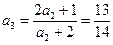 ,
,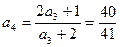 ,
,且
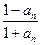
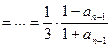 ,
,故
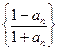 为等比数列,且
为等比数列,且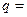
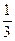 ,
,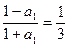
∴
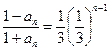 ,∴
,∴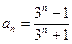 。
。(II)由题设
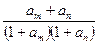 值仅与
值仅与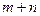 有关,设为
有关,设为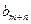 。
。则
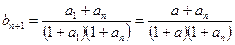 ,
,考察函数
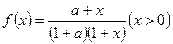 ,则在定义域上有
,则在定义域上有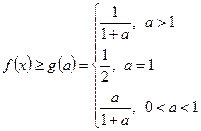
故对
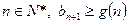 恒成立,又
恒成立,又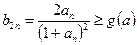 ,
,注意到
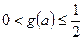 ,解上式得
,解上式得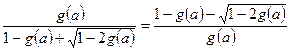
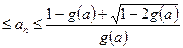 ,
,取
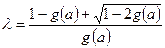 ,即有
,即有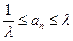 。
。略

练习册系列答案
相关题目
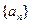 和
和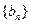 中,数列
中,数列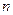 项和记为
项和记为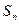 . 若点
. 若点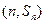 在函数
在函数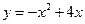 的图象上,点
的图象上,点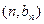 在函数
在函数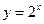 的图象上。
的图象上。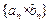 的前
的前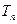
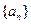 中
中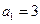 ,
,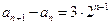
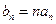 ,求数列
,求数列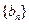 的前
的前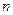 项和
项和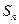
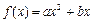 的图像过点
的图像过点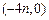 ,且
,且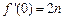 ,
,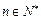 .
.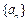 满足
满足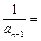
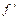
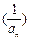 ,且
,且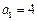 ,求数列
,求数列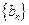 满足:
满足: 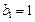 ,
,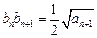 ,当
,当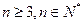 时,
时, 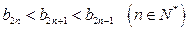 ②
②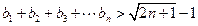
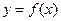 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为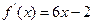 ,数列
,数列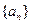 的前n项和为
的前n项和为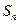 ,点
,点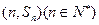 均在函数
均在函数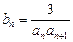 ,
,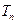 是数列
是数列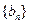 的前n项和,求使得
的前n项和,求使得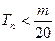 对所有
对所有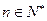 都成立的最小正整数m.
都成立的最小正整数m.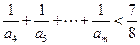
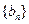 满足
满足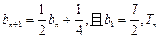 为
为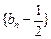 是等比数列,并求
是等比数列,并求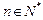 ,不等式
,不等式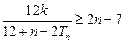 恒成立,求实数
恒成立,求实数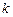 的取值范围.
的取值范围.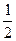 x2+
x2+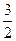 x,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上.
x,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上.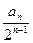 ,求数列{bn}的前n项和Tn
,求数列{bn}的前n项和Tn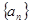 中
中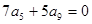 ,且
,且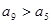 ,则使前
,则使前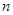 项和
项和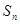 取最小值
取最小值