题目内容
设等比数列{an}满足:Sn=2n+a(n∈N+).
(I)求数列{an}的通项公式,并求最小的自然数n,使an>2010;
(II)数列{bn}的通项公式为bn=-
,求数列{bn}的前n项和Tn.
(I)求数列{an}的通项公式,并求最小的自然数n,使an>2010;
(II)数列{bn}的通项公式为bn=-
| n |
| an |
(I)当n=1时,a1=2+a当n≥2时,an=Sn-Sn-1=2n-1(3分)
∵{an}为等比数列,
∴a1=2+a=21-1=1,
∴a=-1
∴{an}的通项公式为an=2n-1(5分)
令2n-1>2010,又n∈N+,
∴n≥12.
∴最小的自然数n=12(7分)
(II)bn=-
=-
,Tn=-(1•1+2•
+3•
++n•
)①(9分)
Tn=-[1•
+2•
+(n-1)
+n•
]②
②-①得-
Tn=1+
+
++
-n•
,
∴Tn=
-4(14分)
∵{an}为等比数列,
∴a1=2+a=21-1=1,
∴a=-1
∴{an}的通项公式为an=2n-1(5分)
令2n-1>2010,又n∈N+,
∴n≥12.
∴最小的自然数n=12(7分)
(II)bn=-
| n |
| an |
| n |
| 2n-1 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
| 1 |
| 2n |
②-①得-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
| 1 |
| 2n |
∴Tn=
| n+2 |
| 2n-1 |

练习册系列答案
相关题目
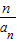 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.