题目内容
设tanα=
,π<α<
,则sinα-cosα的值( )
| ||
| 3 |
| 3π |
| 2 |
A、-
| ||||||
B、-
| ||||||
C、
| ||||||
D、
|
分析:由α的范围得到sinα和cosα都小于0,利用同角三角函数间的基本关系分别求出sinα和cosα的值,代入所求式子中即可求出值.
解答:解:∵tanα=
,π<α<
,
∴cos2α=
=
=
=
,
∴cosα=-
,sinα=-
,
则sinα-cosα=-
-(-
)=-
+
.
故选A
| ||
| 3 |
| 3π |
| 2 |
∴cos2α=
| 1 |
| sec2α |
| 1 |
| 1+tan2α |
| 1 | ||||
1+(
|
| 3 |
| 4 |
∴cosα=-
| ||
| 2 |
| 1 |
| 2 |
则sinα-cosα=-
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
故选A
点评:此题考查了同角三角函数间的基本关系,学生做题时注意角度的范围.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
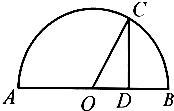 如图,AB是半圆O的直径,点C在半圆上,CD⊥AB于点D,且AD=3DB,设∠COD=θ,则,tanθ=
如图,AB是半圆O的直径,点C在半圆上,CD⊥AB于点D,且AD=3DB,设∠COD=θ,则,tanθ=