题目内容
在体积为4
π的球的表面上有A、B、C三点，AB=1，BC=
，A、C两点的球面距离为
π，则∠ABC=
．
| 3 |
| 2 |
| ||
| 3 |
| π |
| 2 |
| π |
| 2 |
分析：根据球的体积，首先就要先计算出球的半径．再根据A、C两点的球面距离，可求得弧AC所对的圆心角的度数，进而根据余弦定理可得线段AC的长度为
，所以△ABC为直角三角形
| 3 |
解答：解析：设球的半径为R，则V=4
π=
R3，
∴R=
．
设A、C两点对球心张角为θ，则
=Rθ=
θ=
π，
∴θ=
，
∴由余弦定理可得：AC=
，
又∵AB=1，BC=
∴由AC2=AB2+BC2得
∴∠ABC=
故答案为：
| 3 |
| 4π |
| 3 |
∴R=
| 3 |
设A、C两点对球心张角为θ，则
 |
| AC |
| 3 |
| ||
| 3 |
∴θ=
| π |
| 3 |
∴由余弦定理可得：AC=
| 3 |
又∵AB=1，BC=
| 2 |
∴由AC2=AB2+BC2得
∴∠ABC=
| π |
| 2 |
故答案为：
| π |
| 2 |
点评：本小题主要考查立体几何球面距离及点到面的距离，其中根据球体积求出球半径进而求出A、C两点对球心张角是解答的关键．
练习册系列答案
相关题目
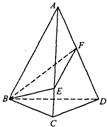如图，已知正三棱锥A-BCD侧面的顶角为40°，侧棱长为a，动点E、F分别在侧棱AC、AD上，则以线段BE、EF、FB长度和的最小值为半径的球的体积为（ ）A、4
| ||
B、
| ||
C、
| ||
| D、4πa3 |