题目内容
（文科）在体积为π4
的球的表面上有A，B，C三点，AB=1，BC=
，A，C两点的球面距离为
π，则球心到平面ABC的距离为（ ）
| 3 |
| 2 |
| ||
| 3 |
分析：根据球的体积，求出球的半径．再根据A、C两点的球面距离，可求得
所对的圆心角的度数，进而根据余弦定理可得线段AC的长度为
，判断△ABC为直角三角形，说明线段AC的中点即为ABC所在平面的小圆圆心，然后求出球心到平面ABC的距离．
 |
| AC |
| 3 |
解答：解：设球的半径为R，则V=
πR3=4
π，
∴R=
．
设A、C两点对球心张角为θ，则
=Rθ=
θ=
π，
∴θ=
，
∴由余弦定理可得：AC=
，
∴AC为ABC所在平面的小圆的直径，
∴∠ABC=90°，
设ABC所在平面的小圆圆心为O'，则球心到平面ABC的距离为d=OO′=
=
=
．
故选C．
| 4 |
| 3 |
| 3 |
∴R=
| 3 |
设A、C两点对球心张角为θ，则
|
| AC |
| 3 |
| ||
| 3 |
∴θ=
| π |
| 3 |
∴由余弦定理可得：AC=
| 3 |
∴AC为ABC所在平面的小圆的直径，
∴∠ABC=90°，
设ABC所在平面的小圆圆心为O'，则球心到平面ABC的距离为d=OO′=
| R2-BO′2 |
3-(
|
| 3 |
| 2 |
故选C．
点评：本小题主要考查立体几何球面距离及点到面的距离．考查空间想象能力，计算能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（文科）已知正四棱柱ABCD-A1B1C1D1中，底面边长为2，AA1=4，点M在线段CC1上．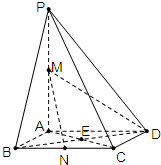
（2008•崇明县一模）（文科）如图，在四棱锥P-ABCD中，底面ABCD是边长为2的正方形，PA⊥底面ABCD，PA=4，M为PA的中点，N为BC的中点．
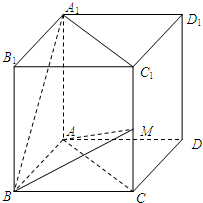（文科）已知正四棱柱ABCD-A1B1C1D1中，底面边长为2，AA1=4，点M在线段CC1上．
，求多面体ABM-A1B1C1的体积．