题目内容
已知两点![]() 、
、![]() 分别在直线
分别在直线![]() 和
和![]() 上运动,且
上运动,且![]() ,动点
,动点![]() 满足
满足![]() (
(![]() 为坐标原点),点
为坐标原点),点![]() 的轨迹记为曲线
的轨迹记为曲线![]() .
.
(1) 求曲线![]() 的方程;
的方程;
(2) 过曲线![]() 上任意一点作它的切线
上任意一点作它的切线![]() ,与椭圆
,与椭圆![]() 交于M、N两点, 求证:
交于M、N两点, 求证:![]() 为定值.
为定值.
【命题意图】本小题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与圆、椭圆的相关知识.
【试题解析】解:⑴(方法一)设![]()
∵![]() ,∴
,∴![]() 是线段
是线段![]() 的中点,∴
的中点,∴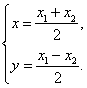 (2分)
(2分)
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∴化简得点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() . (5分)
. (5分)
(方法二)∵![]() ,∴
,∴![]() 为线段
为线段![]() 的中点. (2分)
的中点. (2分)
∵![]() 、
、![]() 分别在直线
分别在直线![]() 和
和![]() 上,∴
上,∴![]() .
.
又![]() ,∴
,∴![]() ,∴点
,∴点![]() 在以原点为圆心,
在以原点为圆心,![]() 为半径的圆上.
为半径的圆上.
∴点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() . (5分)
. (5分)
⑵证明:当直线l的斜率存在时,设l![]() y=kx+m,
y=kx+m,
∵l与C相切,∴![]() =
=![]() ,∴
,∴![]() .
.
联立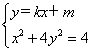 ,∴
,∴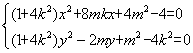 .
.
设M(x1,y1),N(x2,y2),则x1·x2=![]() ,
,![]() . (8分)
. (8分)
∴![]() ·
·![]() =x1x2+y1y2=
=x1x2+y1y2=![]() .
.
又![]() ,∴
,∴![]() ·
·![]() =0. (10分)
=0. (10分)
当直线l的斜率不存在时,l的方程为x=±![]() ,带入椭圆方程得
,带入椭圆方程得
M(![]() ,
,![]() ),N(
),N(![]() ,-
,-![]() ) 或 M(-
) 或 M(-![]() ,
,![]() ),N(-
),N(-![]() ,-
,-![]() ),
),
此时,![]() ·
·![]() =
=![]() -
-![]() =0.
=0.
综上所述,![]() ·
·![]() 为定值0. (12分)
为定值0. (12分)

练习册系列答案
相关题目
 和
和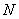 分别在直线
分别在直线 和
和 上运动,且
上运动,且 ,动点
,动点 满足:
满足: 为坐标原点),点
为坐标原点),点
 与曲线。交于不同的两点
与曲线。交于不同的两点 、
、 ,若对于任意
,若对于任意 ,都有
,都有 为锐角,求直线
为锐角,求直线 的取值范围。
的取值范围。