Question

（本小题满分12分）

已知两点、分别在直线和上运动，且，动点满足(为坐标原点)，点的轨迹记为曲线.

(1) 求曲线的方程；(2) 过曲线上任意一点作它的切线，与椭圆交于M、N两点，求证：为定值.

Answer 1

解：⑴(方法一)设

∵，∴是线段的中点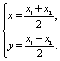，∴　----------2分　　

∵，∴，∴.

∴化简得点的轨迹的方程为.    -----------------5分                            

(方法二)∵，∴为线段的中点. ---------2分　

∵A，B分别在直线和上，∴.

又，∴，∴点在以原点为圆心，为半径的圆上.

∴点的轨迹的方程为.--------------5分                                                      

       ⑵证明：当直线l的斜率存在时，设l y＝kx＋m，

∵l与C相切，∴＝，∴.

联立，∴.---------------6分

设M(x₁，y₁)，N(x₂，y₂)，则x₁·x₂＝，.-------------8分　

又，∴·＝0.　--------------------------10分

当直线l的斜率不存在时，l的方程为x＝±，带入椭圆方程得

M(，)，N(，－) 或 M(－，)，N(－，－)，

此时，·＝－＝0.

综上所述，·为定值0. ------------------12分