题目内容
(本小题满分12分) 已知两点![]() 和
和![]() 分别在直线
分别在直线![]() 和
和![]()
![]() 上运动,且
上运动,且![]() ,动点
,动点![]() 满足:
满足:![]() (
(![]() 为坐标原点),点
为坐标原点),点![]() 的轨迹记为曲线
的轨迹记为曲线![]() . (Ⅰ)求曲线
. (Ⅰ)求曲线![]() 的方程,并讨论曲线
的方程,并讨论曲线![]() 的类型; (Ⅱ)过点
的类型; (Ⅱ)过点![]() 作直线
作直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,若对于任意
,若对于任意![]() ,都有
,都有![]() 为锐角,求直线
为锐角,求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
(Ⅰ) 当![]() 时,方程表示焦点在
时,方程表示焦点在![]() 轴上的椭圆;当
轴上的椭圆;当![]() 时,方程表示焦点在
时,方程表示焦点在![]() 轴上的椭圆;当
轴上的椭圆;当![]() 时,方程表示圆. (Ⅱ)
时,方程表示圆. (Ⅱ) ![]()
解析:
(I)由![]() ,得
,得![]() 是
是![]() 的中点. …………………2分
的中点. …………………2分
设![]() 依题意得:
依题意得:
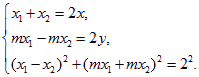 消去
消去![]() ,整理得
,整理得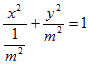 .…………………4分
.…………………4分
当![]() 时,方程表示焦点在
时,方程表示焦点在![]() 轴上的椭圆;当
轴上的椭圆;当![]() 时,方程表示焦点在
时,方程表示焦点在![]() 轴上的椭圆;
轴上的椭圆;
当![]() 时,方程表示圆.……………5分
时,方程表示圆.……………5分
(II)由![]() ,焦点在
,焦点在![]() 轴上的椭圆,直线
轴上的椭圆,直线![]() 与曲线
与曲线![]() 恒有两交点,
恒有两交点,
因为直线斜率不存在时不符合题意,
可设直线![]() 的方程为
的方程为![]() ,直线与椭圆的交点为
,直线与椭圆的交点为![]() .
.
 …………………7分
…………………7分
![]()
![]()
![]()
要使![]() 为锐角,则有
为锐角,则有![]() …………………9分
…………………9分
![]() 即
即![]() ,
,
可得![]() ,对于任意
,对于任意![]() 恒成立.而
恒成立.而![]() ,
,![]()
所以满足条件的![]() 的取值范围是
的取值范围是![]() .…………………12分
.…………………12分

练习册系列答案
相关题目