题目内容
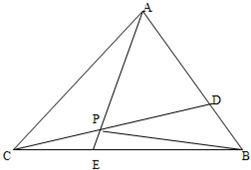
如图，已知△ABC的面积为14，D、E分别为边AB、BC上的点，且AD：DB=BE：EC=2：1，AE与CD交于P．设存在λ和μ使| AP |
| AE |
| PD |
| CD |
| AB |
| a |
| BC |
| b |
（1）求λ及μ；
（2）用
| a |
| b |
| BP |
（3）求△PAC的面积．
分析：（1）根据
=λ
=λ(
+
)，用基底
、
表示出
．再根据
=
+
=
+
，
用基底
、
表示出
．这两种表示方式是相同的，由此求出λ及μ．
（2）把
用
+
来表示，把（1）中的结果代入可得用基底
、
表 示的
．
（3） 根据面积之比等于对应的向量的长度比求出△PAB和△PBC 的面积，用△ABC的面积减去△PAB和△PBC 的面积
即得△PAC的面积．
| AP |
| AE |
| a |
| 2 |
| 3 |
| b |
| a |
| b |
| AP |
| AP |
| AD |
| DP |
| 2 |
| 3 |
| AB |
| DP |
用基底
| a |
| b |
| AP |
（2）把
| BP |
| BA |
| AP |
| a |
| b |
| BP |
（3） 根据面积之比等于对应的向量的长度比求出△PAB和△PBC 的面积，用△ABC的面积减去△PAB和△PBC 的面积
即得△PAC的面积．
解答：解：（1）由于
=
，
=
，则
=
+
，
=
+
，
=λ
=λ(
+
)，
=μ
=μ(
+
)，
=
+
=
+
，
+μ(
+
)=λ(
+
)，∴λ=
+
μ ①，
λ=μ ②，
由①②得λ=
，μ=
（2）
=
+
=-
+
×(
+
)=-
+
．
（3）设△ABC，△PAB，△PBC的高分别为h，h1，h2，
h1：h=|
|：|
|=μ=
，S△PAB=
S△ABC=8，
h2：h=|
|：|
|=1-λ=
，S△PBC=
S△ABC=2，S△PAC=4．
| AB |
| a |
| BC |
| b |
| AE |
| a |
| 2 |
| 3 |
| b |
| DC |
| 1 |
| 3 |
| a |
| b |
| AP |
| AE |
| a |
| 2 |
| 3 |
| b |
| DP |
| DC |
| 1 |
| 3 |
| a |
| b |
| AP |
| AD |
| DP |
| 2 |
| 3 |
| AB |
| DP |
| 2 |
| 3 |
| a |
| 1 |
| 3 |
| a |
| b |
| a |
| 2 |
| 3 |
| b |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
由①②得λ=
| 6 |
| 7 |
| 4 |
| 7 |
（2）
| BP |
| BA |
| AP |
| a |
| 6 |
| 7 |
| a |
| 2 |
| 3 |
| b |
| 1 |
| 7 |
| a |
| 4 |
| 7 |
| b |
（3）设△ABC，△PAB，△PBC的高分别为h，h1，h2，
h1：h=|
| PD |
| CD |
| 4 |
| 7 |
| 4 |
| 7 |
h2：h=|
| PE |
| AE |
| 1 |
| 7 |
| 1 |
| 7 |
点评：本题考查向量数乘的运算和几何意义，把三角形的面积之比转化为向量的长度比，是解题的难点．
练习册系列答案
相关题目
如图，已知△ABC的顶点坐标依次为A（1，0），B（5，8），C（7，-4），在边AB上有一点P，其横坐标为4，在AC上求一点Q，使线段PQ把△ABC分成面积相等的两部分．
如图，已知△ABC的顶点为A（2，4），B（0，-2），C（-2，3），求：
如图，已知△ABC的外角∠EAC的平分线与△ABC的外接圆交于点D，以CD为直径的圆分别交BC，CA于点P、Q，求证：线段PQ平分△ABC的周长．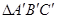
是边长为2的正三角形，则原△ABC的面积为__________.