Question

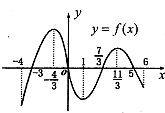已知函数y=f（x）在定义域[-4，6]图象如图，记y=f（x）y=f′（x），则不等式f′（x）≥0的解集为（　　）

• A、[-

  4

  3

  ，1]∪[

  11

  3

  ，6]
• B、[-3，0]∪[

  7

  3

  ，5]
• C、[-4，-

  4

  3

  ]∪[1，

  11

  3

  ]
• D、[-4，3]∪[0，1]∪[5，6]

Answer 1

分析：由图象求函数的单调区间，据单调性与导数符号的关系求解．

解答：解：由函数y=f（x）在定义域[-4，6]图象知，y=f（x）的单调递增区间为[-4，-

4

3

]和[1，

11

3

]
所以不等式f′（x）≥0的解集为[-4，-

4

3

]∪[1，

11

3

]

点评：函数单调递增时导数大于零，函数单调递减时导数小于零．