题目内容
已知定义在R上的奇函数f(x),当x>0时有f(x)=(
)x-x3,则当x<0时f(x)= .
| 1 |
| 2 |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:设x<0,则-x>0.由于当x>0时有f(x)=(
)x-x3,可得f(-x)=(
)-x+x3=2x+x3.再利用奇函数的性质即可得出.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:设x<0,则-x>0.
∵当x>0时有f(x)=(
)x-x3,
∴f(-x)=(
)-x+x3=2x+x3.
∵定义在R上的奇函数f(x),
∴f(x)=-f(-x)=-2x-x3.
故答案为:-2x-x3.
∵当x>0时有f(x)=(
| 1 |
| 2 |
∴f(-x)=(
| 1 |
| 2 |
∵定义在R上的奇函数f(x),
∴f(x)=-f(-x)=-2x-x3.
故答案为:-2x-x3.
点评:本题考查了奇函数的性质,属于基础题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
设α为锐角,且cos(α+
)=
,则sin(α-
)的值为( )
| π |
| 3 |
| 4 |
| 5 |
| π |
| 6 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
等差数列{an}的公差d<0,且a12=a20142,若数列{an}的前n项和Sn最大,Sm=0,则m-n的值为( )
| A、1007 | B、1006 |
| C、1005 | D、1004 |
如图,若输入n的值为4,则输出A的值为( )


| A、3 | ||
| B、-2 | ||
C、-
| ||
D、
|
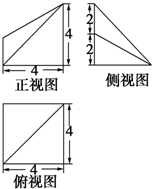 已知某几何体的三视图如图所示,则该几何体的体积为( )
已知某几何体的三视图如图所示,则该几何体的体积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
下列选项的对象中能构成集合的为( )
| A、一切很大的数 |
| B、聪明人 |
| C、正三角形的全体 |
| D、高一教材中的所有难题 |
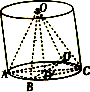 在一个圆柱中挖去一个内接正四棱锥O-ABCD(顶点是上面底面积圆的圆心O,底面是下底面的内接正方形),得到如图所示的几何体,已知圆柱底面直径为4
在一个圆柱中挖去一个内接正四棱锥O-ABCD(顶点是上面底面积圆的圆心O,底面是下底面的内接正方形),得到如图所示的几何体,已知圆柱底面直径为4