题目内容
20. 已知函数$f(x)=\frac{x+2}{x-2}$.
已知函数$f(x)=\frac{x+2}{x-2}$.(1)在下列坐标系中作出函数f(x)的大致图象;
(2)将函数f(x)的图象向下平移一个单位得到函数g(x)的图象,点A是函数g(x)图象的上一点,B(4,-2),求|AB|的最小值.
分析 (1)因为$f(x)=\frac{x+2}{x-2}=1+\frac{4}{x-2}$,故把函数y=$\frac{4}{x-2}$的图象向上平移1个单位,可得函数$f(x)=\frac{x+2}{x-2}$的图象,如图所示.
(2)计算|AB|2=${[{({{x_0}-2})-({\frac{4}{{{x_0}-2}}})}]^2}-4[{({{x_0}-2})-({\frac{4}{{{x_0}-2}}})}]+16$,令$({{x_0}-2})-({\frac{4}{{{x_0}-2}}})=t$,可得|AB|2=t2-4t+16,利用二次函数的性质求得它的最小值.
解答 解:(1)因为$f(x)=\frac{x+2}{x-2}=1+\frac{4}{x-2}$,故把函数y=$\frac{4}{x-2}$的图象向上平移1个单位,
可得函数$f(x)=\frac{x+2}{x-2}$的图象,故函数$f(x)=\frac{x+2}{x-2}$的大致图象如图所示: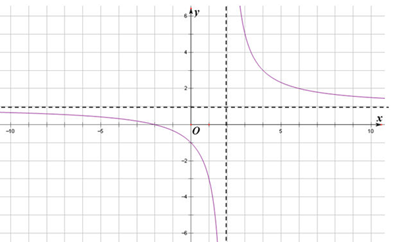
(2)依题意,函数$g(x)=\frac{4}{x-2}$,设$A({{x_0},\frac{4}{{{x_0}-2}}})$,因为B(4,-2),
故${|{AB}|^2}={({{x_0}-4})^2}+{({\frac{4}{{{x_0}-2}}+2})^2}={({{x_0}-2})^2}-4({{x_0}-2})+4+{({\frac{4}{{{x_0}-2}}})^2}+\frac{16}{{{x_0}-2}}+4$=${[{({{x_0}-2})-({\frac{4}{{{x_0}-2}}})}]^2}-4[{({{x_0}-2})-({\frac{4}{{{x_0}-2}}})}]+16$,
令$({{x_0}-2})-({\frac{4}{{{x_0}-2}}})=t$,故|AB|2=t2-4t+16=(t-2)2+12≥12,当且仅当t=2时,
此时方程$({{x_0}-2})-({\frac{4}{{{x_0}-2}}})=2$有解,|AB|2取得最小值为12,故|AB|的最小值为$2\sqrt{3}$.
点评 本题主要考查函数的图象,二次函数的性质,求函数的最值,属于中档题.

 阅读快车系列答案
阅读快车系列答案| 学生 | A | B | C | D | E |
| 数学 | 80 | 75 | 70 | 65 | 60 |
| 物理 | 70 | 66 | 68 | 64 | 62 |
(2)若小红这次考试的数学成绩是52分,你估计她的物理成绩是多少分呢?供参考的数据:80×70+75×66+70×68+65×64+60×62=23190;802+752+702+652+602=24750.
| A. | $\frac{\sqrt{113}}{2}$ | B. | 5 | C. | $\sqrt{41}$ | D. | 25 |
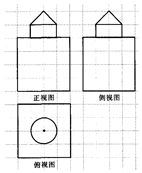 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积为( )| A. | $({2\sqrt{2}+2})π+96$ | B. | $({2\sqrt{2}+1})π+96$ | C. | $({\sqrt{2}+2})π+96$ | D. | $({\sqrt{2}+1})π+96$ |