题目内容
【题目】已知椭圆
：
的左、右焦点分别为
，
是椭圆上的点，且
的面积为
。
（1）求椭圆的方程；
（2）若斜率为
且在
轴上的截距为
的直线
与椭圆相交于两点
，若椭圆上存在点
，满足
，其中
是坐标原点，求的值。
【答案】（1）
； （2）
.
【解析】
（1）利用已知条件列出椭圆几何量的方程组，求解a，b，即可求椭圆C的方程；
（2）联立直线与椭圆方程，利用韦达定理，结合向量关系，推出结果即可．
（1）∵△PF1F2的面积为
，∴
×2c×＝，即c＝1，
由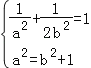
，解得a2＝2，b2＝1，∴椭圆C的方程为
+y2＝1；
（2）由题意可得l：y＝k（x﹣2），设点A（x1，y1），B（x2，y2），Q（x，y），
由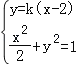
，消y可得（1+2k2）x2﹣8kx+8k2﹣2＝0，
∴△＝64k2﹣4（1+2k2）（8k2﹣2）＞0，可得k2＜
，
∴x1+x2＝
，x1x2＝
，
∵
，∴
＝3
﹣3（
﹣
），即＝
（+
），
∴（x，y）＝
（x1+x2，y1+y2），∴x＝（x1+x2）＝
y＝[k（x1+x2）﹣4k]＝
，∴Q（
，
），∵点Q在椭圆C上，
∴
+2
＝2，∴9k2＝1+2k2，解得k＝±
．
练习册系列答案
相关题目
【题目】下表提供了工厂技术改造后某种型号设备的使用年限x和所支出的维修费y（万元）的几组对照数据：
x（年） | 2 | 3 | 4 | 5 | 6 |
y（万元） | 1 | 2.5 | 3 | 4 | 4.5 |
（1）若知道y对x呈线性相关关系，请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程
；
（2）已知该工厂技术改造前该型号设备使用10年的维修费用为9万元，试根据（1）求出的线性回归方程，预测该型号设备技术改造后，使用10年的维修费用能否比技术改造前降低?
参考公式：
，
.
