题目内容
(1) 若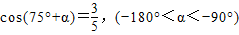 ,求sin(105°-α)+cos(375°-α)值;
,求sin(105°-α)+cos(375°-α)值;(2) 在△ABC中,若
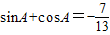 ,求sinA-cosA,tanA的值.
,求sinA-cosA,tanA的值.
【答案】分析:(1)∵105°-α=180°-(75°+α),375°-α=360°+(15°-α),我们根据诱导公式结合已知中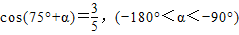 ,即可求出sin(105°-α)+cos(375°-α)的值;
,即可求出sin(105°-α)+cos(375°-α)的值;
(2)由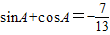 ,由A为三角形的内角,则A为钝角,结合平方关系,我们不难求出sinA-cosA,tanA的值.
,由A为三角形的内角,则A为钝角,结合平方关系,我们不难求出sinA-cosA,tanA的值.
解答:解:(1)sin(105°-α)=sin[180°-(75°+α)]=sin(75°+α)
∵-180°<α<-90°
∴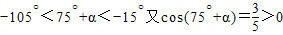
∴-90°<75°+α<-15°
∴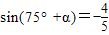

∴原式=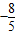
(2)由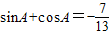 两边平方得
两边平方得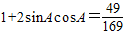
而0<A<π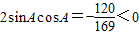
∴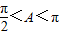
∴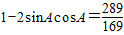
即
又sinA-cosA>0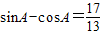
∴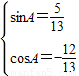
∴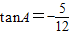
点评:本题考查的知识点是三角函数如恒等变换应用,运用诱导公式化简求值,同角三角函数关系等,分析已知角与未知角之间的关系,以选择恰当的公式进行化简求值是三角函数求值中最关键的环节.
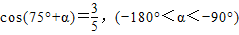 ,即可求出sin(105°-α)+cos(375°-α)的值;
,即可求出sin(105°-α)+cos(375°-α)的值;(2)由
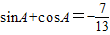 ,由A为三角形的内角,则A为钝角,结合平方关系,我们不难求出sinA-cosA,tanA的值.
,由A为三角形的内角,则A为钝角,结合平方关系,我们不难求出sinA-cosA,tanA的值.解答:解:(1)sin(105°-α)=sin[180°-(75°+α)]=sin(75°+α)
∵-180°<α<-90°
∴
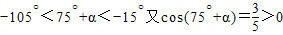
∴-90°<75°+α<-15°
∴
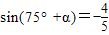

∴原式=
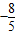
(2)由
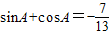 两边平方得
两边平方得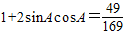
而0<A<π
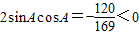
∴
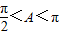
∴
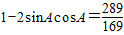
即

又sinA-cosA>0
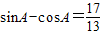
∴
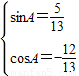
∴
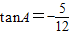
点评:本题考查的知识点是三角函数如恒等变换应用,运用诱导公式化简求值,同角三角函数关系等,分析已知角与未知角之间的关系,以选择恰当的公式进行化简求值是三角函数求值中最关键的环节.

练习册系列答案
相关题目
 =(2,sinθ),
=(2,sinθ), =(1,cosθ),θ为锐角.
=(1,cosθ),θ为锐角. ,求sinθ+cosθ的值;
,求sinθ+cosθ的值; )的值.
)的值.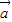 =(2,sinθ),
=(2,sinθ),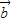 =(1,cosθ),θ为锐角.
=(1,cosθ),θ为锐角.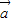 •
•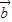 =
=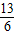 ,求sinθ+cosθ的值;
,求sinθ+cosθ的值;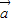 ∥
∥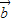 ,求sin(2θ+
,求sin(2θ+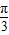 )的值.
)的值.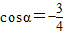 ,求sinα和tanα的值;(2)化简
,求sinα和tanα的值;(2)化简 •tanα
•tanα =(2,sinθ),
=(2,sinθ),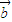 =(1,cosθ),θ为锐角.
=(1,cosθ),θ为锐角.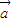 •
• =
=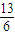 ,求sinθ+cosθ的值;
,求sinθ+cosθ的值;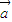 ∥
∥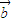 ,求sin(2θ+
,求sin(2θ+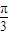 )的值.
)的值.