题目内容
设向量 =(2,sinθ),
=(2,sinθ),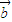 =(1,cosθ),θ为锐角.
=(1,cosθ),θ为锐角.(1)若
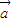 •
• =
=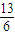 ,求sinθ+cosθ的值;
,求sinθ+cosθ的值;(2)若
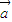 ∥
∥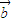 ,求sin(2θ+
,求sin(2θ+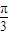 )的值.
)的值.
【答案】分析:(1)根据向量数量积的坐标公式列式并化简,得sinθcosθ= .再由同角三角函数的平方关系,可得(sinθ+cosθ)2的值,结合θ为锐角,开方即得sinθ+cosθ的值;
.再由同角三角函数的平方关系,可得(sinθ+cosθ)2的值,结合θ为锐角,开方即得sinθ+cosθ的值;
(2)根据两个向量平行的充要条件列式,化简得tanθ=2.再由二倍角的正、余弦公式,结合弦化切的运算技巧,算出sin2θ和cos2θ的值,最后根据两角和的正弦公式,可得sin(2θ+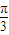 )的值.
)的值.
解答:解:(1)∵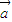 •
•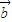 =2+sinθcosθ=
=2+sinθcosθ=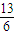 ,∴sinθcosθ=
,∴sinθcosθ= . …(2分)
. …(2分)
∴(sinθ+cosθ)2=1+2sinθcosθ= .
.
又∵θ为锐角,∴sinθ+cosθ=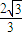 (舍负). …(5分)
(舍负). …(5分)
(2)∵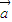 ∥
∥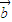 ,
,
∴2×cosθ=sinθ×1,可得tanθ=2. …(7分)
∴sin2θ=2sinθcosθ=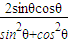 =
=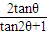 =
=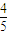 ,
,
cos2θ=cos2θ-sin2θ=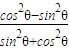 =
=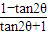 =-
=-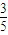 .…(11分)
.…(11分)
所以sin(2θ+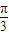 )=
)= sin2θ+
sin2θ+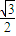 cos2θ=
cos2θ= ×
×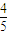 +
+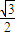 ×(-
×(-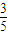 )=
)=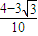 . …(14分)
. …(14分)
点评:本题以平面向量数量积运算为载体,考查了同角三角函数的基本关系、二倍角的正余弦公式和两角和的正弦公式等知识,属于中档题.
 .再由同角三角函数的平方关系,可得(sinθ+cosθ)2的值,结合θ为锐角,开方即得sinθ+cosθ的值;
.再由同角三角函数的平方关系,可得(sinθ+cosθ)2的值,结合θ为锐角,开方即得sinθ+cosθ的值;(2)根据两个向量平行的充要条件列式,化简得tanθ=2.再由二倍角的正、余弦公式,结合弦化切的运算技巧,算出sin2θ和cos2θ的值,最后根据两角和的正弦公式,可得sin(2θ+
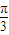 )的值.
)的值.解答:解:(1)∵
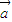 •
•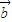 =2+sinθcosθ=
=2+sinθcosθ=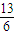 ,∴sinθcosθ=
,∴sinθcosθ= . …(2分)
. …(2分)∴(sinθ+cosθ)2=1+2sinθcosθ=
 .
.又∵θ为锐角,∴sinθ+cosθ=
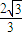 (舍负). …(5分)
(舍负). …(5分)(2)∵
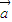 ∥
∥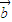 ,
,∴2×cosθ=sinθ×1,可得tanθ=2. …(7分)
∴sin2θ=2sinθcosθ=
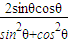 =
=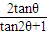 =
=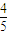 ,
,cos2θ=cos2θ-sin2θ=
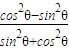 =
=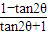 =-
=-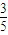 .…(11分)
.…(11分)所以sin(2θ+
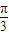 )=
)= sin2θ+
sin2θ+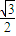 cos2θ=
cos2θ= ×
×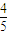 +
+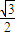 ×(-
×(-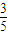 )=
)=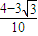 . …(14分)
. …(14分)点评:本题以平面向量数量积运算为载体,考查了同角三角函数的基本关系、二倍角的正余弦公式和两角和的正弦公式等知识,属于中档题.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
 ,
,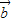 =(2,sinα),若
=(2,sinα),若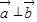 ,则tan(α-
,则tan(α-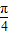 )等于( )
)等于( )
