题目内容
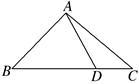
如图,在△ABC中,已知∠B=45°,D是BC边上的一点,AD=10,AC=14,DC=6,求AB的长.

5 .
.
 .
.试题分析:由于△ADC的三边长都已知,所以在△ADC应用余弦定理可求得
 的余弦值,进而就可求得
的余弦值,进而就可求得 的正弦值,然后在
的正弦值,然后在 应用正弦定理可求出AB的长.注意
应用正弦定理可求出AB的长.注意 应为钝角,
应为钝角, 为锐角.
为锐角.试题解析:在△ADC中,AD=10,AC=14,DC=6,由余弦定理得cos∠ADC=

=
 =-
=- ,∴∠ADC=120°,∴∠ADB=60°.
,∴∠ADC=120°,∴∠ADB=60°.在△ABD中,AD=10,∠B=45°,∠ADB=60°,
由正弦定理得
 =
= ,∴AB=
,∴AB= =
= =
= =5
=5 .
.
练习册系列答案
相关题目
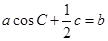 .
.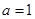 ,求△ABC的周长L的取值范围.
,求△ABC的周长L的取值范围.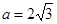 ,
,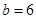 ,
,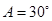 ,求B及S
,求B及S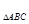 .
.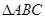 中,角
中,角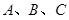 所对的边为
所对的边为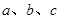 ,且满足
,且满足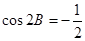 ,
,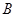 的值;(2)若
的值;(2)若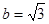 且
且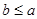 ,求
,求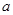 的取值范围.
的取值范围.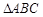 中,
中,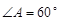 ,
,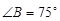 ,
,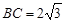 ,则
,则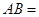 .
. ,且a + b = 5,
,且a + b = 5, ,则△ABC的面积为( )
,则△ABC的面积为( ) B.
B. C.
C. D.
D.
 中,内角
中,内角 的对边分别为
的对边分别为 ,若
,若 ,
, ,
, ,则
,则 等于( )
等于( )
